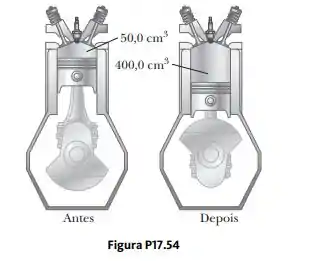
Durante a partida do motor de um automóvel de quatro tempos, o pistão é forçado para baixo enquanto a mistura de produtos da combustão e do ar sofre uma expansão adiabática. Suponha que (1) o motor esteja funcionando em 2500 ciclos/min, (2) a pressão do manômetro imediatamente antes da expansão seja 20,0 atm, (3) os volumes da mistura imediatamente antes e após a expansão sejam 50,0 cm3 e 400 cm3, respectivamente (Fig. P17.54), (4) o intervalo de tempo para a expansão seja de um quarto do ciclo total, e (5) a mistura se comporte como um gás ideal em relação ao calor específico 1,40. Encontre a potência média gerada durante a partida do motor.

Falaaaaaaaaaaaaaaaa Tribuxo?

Bora resolver mais uma questão!?

Para resolver essa questão iremos usar:

Podemos achar :

Como é adiabático:

Então:

Temos:

Podemos achar :

Sendo :

Então:

Podemos achar :

O gás é diatômico:

Então:

Podemos fazer:

Então:

Podemos achar :

Isolando :

Convertendo: