Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alonso e Finn - Campos e Ondas- Ed: 2º - Capítulo 14.Problemas - Ex. 11

Um elétron é projetado em um campo elétrico uniforme de intensidade 5000 N C-1. A direção do campo é verticalmente para baixo. A velocidade inicial do elétron é 10^7 m/s', em um ângulo de 30 ° acima da horizontal. (a) Calcule o tempo necessário para o elétron atingir seu máximo de altura. (b) Calcule a distância que o elétron sobe verticalmente acima da sua elevação inicial. (c) Depois de qual distância horizontal o elétron retorna à sua elevação original? (d) Esboce a trajetória do elétron.

Passo 1

Fala galera, tudo bom com vocês?

Vem comigo pra fazer essa questãozinha aqui!

Como E → está para baixo, então F → = - e E - , e disso deduzimos que F → terá seu sentido para cima. Devemos fazer a análise vetorial para não ter problemas.

Logo,

F = - e E = m a

E nesse caso usamos o módulo somente porque já sabemos o sentido.

e E = m a

a = e E m → a = 1.6021 × 10 - 19 × 5000 9.1091 × 10 - 31 m / s

a = 8.7939 × 10 14 m s                                 ( 1 )

Agora vamos analisar a velocidade do elétron:

v o x = v 0 c o s ⁡ 30 ∘ v oy   = v 0 s e n ⁡ 30 ∘

Passo 2

Letra a:

Aplicando a seguinte fórmula, obtemos o tempo:

v f = v o y + a t

0 = V 0 s i n 30 ∘ + 8.7939 × 10 14 × t

t = 10 7 × 0.5 8.7939 × 10 14

t = 5.6857 × 10 - 9 s

Passo 3

Letra b:

Calculando o alcance máximo (elevação):

v f 2 = v oy  2 + 2 a h

h = v o y 2 2 a

h = 0.5 × 10 7 2 2 × 8.7934 × 10 14 m

h = 1.421 × 10 - 2 m

Passo 4

Letra c:

A distância será = velocidade vezes tempo:

velocidade   = V o x  = 0.8660 × 10 7 m s

tempo  =  tempo subida  +  tempo de  descida

= 2 t = 2 × 5.6857 × 10 - 9 s

Finalmente,

d = V o x ⋅ ( 2 t ) d = 0.8660 × 10 7 × 2 × 5.6857 × 10 - 9 m

a = 9.8479 × 10 - 2 m

Passo 5

Letra d:

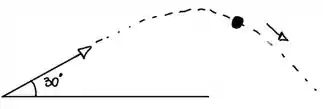
Resposta

  1. t = 5.6857 × 10 - 9 s
  2. h = 1.421 × 10 - 2 m
  3. a = 9.8479 × 10 - 2 m
  4. Ver diagrama
Ver Outros Exercícios desse livro