Enquanto se muda, um novo proprietário está empurrando uma caixa através do piso a uma velocidade constante. O coeficiente de atrito cinético entre a caixa e o piso é 0,41. A força de empuxo é direcionada para baixo em um ângulo abaixo da horizontal. Quando é maior que um certo valor, não é possível mover a caixa, não importa quão grande seja a força de empuxo é. Encontre esse valor de .

O diagrama de corpo livre para a caixa é mostrado na figura abaixo. Na direita, a força é decomposta em suas componentes vertical e horizontal.

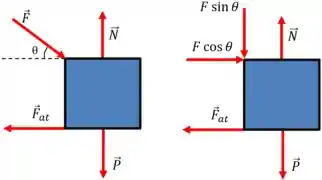
Já que a caixa está se movendo em uma velocidade constante, ela não possui aceleração, e a segunda lei de Newton indica que a força resultante vertical e horizontal devem, separadamente, dar zero.

Tomando como positivo a direção para cima e para direita, nós escrevemos a força resultante vertical e horizontal e igualamos a zero:

Vertical:

Horizontal:

Da equação para forças horizontais, temos que

E a força de atrito é

Da equação para forças verticais, temos que

Para isso, podemos ter

E resolvendo para :

A força necessária tende ao infinito quando o denominador na expressão que achamos para é zero. Então, temos que

Em que podemos rearranjar para

Ou