Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 30.Exercícios e Problemas - Ex. 50
Uma esfera metálica 1 possui uma carga positiva de . Outra esfera metálica 2, com diâmetro duas vezes maior do que o da esfera 1 está inicialmente descarregada. As esferas são, então, conectadas por um fio metálico fino e longo. Quais são as cargas finais em cada esfera?
Passo 1
Faaaaaala, galera... Tranquileba??
Desenhando a figura dada no enunciado temos:
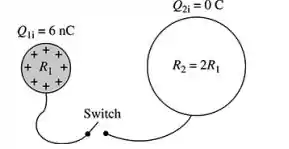
A princípios sabemos que a carga final da soma de ambas deve ser o mesmo
E a carga na primeira esfera após a conexão deve ser
Assim:
E sabemos que o potencial de uma esfera é dada por:
Passo 2
Busquemos achar as cargas finais das esferas, sabendo que quando conectadas, ambas terão o mesmo potencial ou seja, diferença de potencial igual a 0
E sabemos que quando conectadas, a carga deve ser conservativa. Portanto:
Passo 3
Lembrando que
Logo:
E se a carga final da esfera pequena é de , a da esfera grande é de:
Resposta
Para a esfera pequena:
E para a esfera grande: