Em um experimento para confirmar o momento angular de um sistema rotacional, um estudante obtém os resultados apresentados na Tabela 2.6, para os momentos angulares iniciais e finais (L e L’). Introduza uma coluna extra na tabela para mostrar a diferença L-L��� e sua incerteza. Os resultados do estudante estão consistentes com a conservação do momento angular?
Passo 1
Pela regra provisória, sabemos que ao realizar uma diferença, a incerteza dos resultados será igual à soma das incertezas dadas por cada elemento. Temos a tabela:
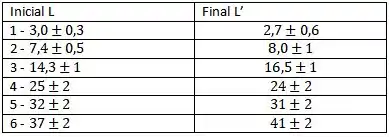
Vamos calcular, um por um, o valor da diferença:
Colocando na tabela, teremos:
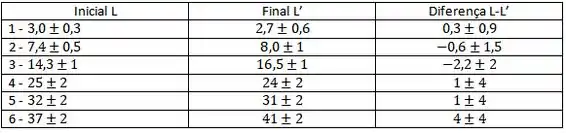
Passo 2
Como podemos ver, todos os valores finais de L-L’, exceto o terceiro, obtiveram incertezas maiores que os valores medidos. Por conta disso, os valores são sim condizentes ao esperado, que é zero.
Resposta
As diferenças L-L’ estão na tabela abaixo:
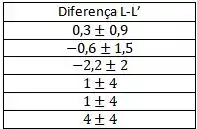
Sim, os valores foram condizentes ao esperado para os momentos.