Faça um gráfico, semelhante ao da fig. 8.19, de Epel para Ep(r)=1/r (a) Epc = 1/2r² (b) Epc = 2/r² onde todas as energias são dadas em J e r em m. Determine a posição ele mínimo para E r em cada caso. "Meça" a energia necessária para ir do mínimo da primeira curva ao mínimo da segunda.
Passo 1
Oiii galeraa!!! Vamos entender o gráfico deste movimento:
Como sabemos de 8.12, precisamos partir da equação:
Derivando este valor e igualando a zero, temos:
Passo 2
Logo, r0=1 é o nosso ponto de mínima. Quando r tende a 2, as energias tendem a zero. E quando as energias tendem a 2, r tende a 0. Logo, as retas Ep=0 e r=0 são assíntotas da curva. De todas as curvas, a única que corta r é a da energia potencial elástica. Assim, temos o seguinte gráfico:
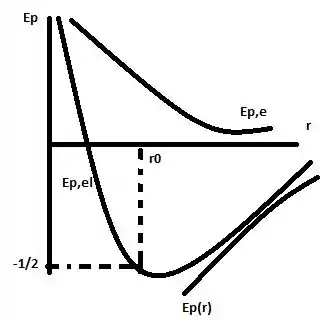
Resposta
Resposta acima.