Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Termodinâmica Óptica- Ed: 2º - Capítulo 23.Exercícios e Problemas - Ex. 82

Um feixe de luz branca penetra em um material transparente. Comprimentos de onda de luz para os quais o índice de refração é n são refratados segundo o ângulo θ 2 . Comprimentos de onda para os quais o índice de refração é n   +   δ n , onde δ n   < <   n , são refratados com ângulo θ 2 +   δ θ .

  1. Demonstre que a separação angular, em radianos, é dada por δ θ = - t g ( θ n / n )   .

  2. Um feixe de luz branca incide sobre um pedaço de vidro segundo 30,0°. A luz violeta escura é refratada em 0,28° a mais do que a luz vermelha intensa. O índice de refração da luz vermelha escura é 1,552. Qual é o índice de refração para a luz violeta escura?

Passo 1

a)

Adivinha só? Nós vamos desenvolver essa questão pelo modelo de raios de luz, bora relembrar? A imagem abaixo mostra o efeito da refração, ou seja, na parte de cima temos um raio de luz incidindo sobre um ângulo θ 1 em um ambiente com índice de refração 1, esse mesmo feixe de luz passa pra outro ambiente na qual o índice de refração passa a ser n, assim, o ângulo de propagação do feixe também muda para θ 2 .

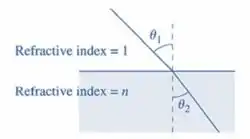
De acordo com a Lei de Refração (a galerinha também chama de lei de Snell), segundo ela o seno do ângulo inicial é igual o índice de refração inicial vezes o ângulo de refração final, ou seja, s e n θ 1 = n   s e n ( θ 2 ) .

Passo 2

Interpretando a questão a partir do modelo de raios de luz, temos que no momento de refração, quando o raio de luz incide com índice de refração de n   +   δ n , a refração ocorre com o ângulo de θ 2 + δ θ .

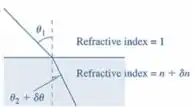
Passo 3

Aplicando a Lei de Refração, temos que s e n θ 1 = ( n   +   δ n ) s e n ( θ 2 +   δ θ ) . No passo 1, nós vimos que s e n θ 1 = n   s e n ( θ 2 ) , então igualando as equações:

n   s e n θ 2 = n   +   δ n s e n θ 2 +   δ θ = n   +   δ n s e n   θ 2 c o s c o s   δ θ   + c o s c o s     θ 2     s e n   δ θ = n   +   δ n ( s e n     θ 2 + c o s c o s     θ 2   δ θ   )

Lembra que o enunciado pediu para considerarmos δ n   < <   n , sabendo disso, vamos continuar desenvolvendo a multiplicação dos termos:

n   s e n θ 2 = n s e n   θ 2 + n c o s   θ 2 δ θ + δ n s e n   θ 2 + δ n δ θ c o s c o s   θ 2  

Podemos ignorar o último termo da direita pois estamos multiplicando dois termos muuuito pequeninos, quase zero, logo:

n c o s   θ 2 δ θ = - δ n s e n   θ 2       →       δ θ = - t a n t a n   θ 2     δ n n

Note que a questão pede o ângulo em radianos, se formos transformar, perceberemos que o radiano tem o mesmo valor de ângulo, logo, terminamos a questão!!!

Passo 4

b)

Na situação expressa no item b), nós temos um ´raio de luz incidindo com θ 1 = 30 ° e índice de refração de 1,552, sabendo que o comprimento de onda vermelha é maior do que o comprimento de onda violeta, então n v e r m e l h o < n v i o l e t a . Se o ângulo de refração da luz vermelha é θ 2 , logo, o ângulo de refração da luz violeta é menor que θ 2 .

Passo 5

Para determinarmos θ 2 , usaremos a expressão do passo 1:

n v e r m e l h o   s e n θ 2 = n v i o l e t a   s e n   30 °       →       θ 2 = s e n - 1 s e n   30 ° 1,552 = 18,794 °       →     t a n t a n   θ 2   = 0,3403

E por fim, vamos só aplicar na equação que obtivemos no item a), substituindo δ θ   =   - 0.28 ° temos que

δ θ = - t a n t a n   θ 2     δ n n = - n t a n t a n   θ 2   δ θ = - 1,552 0,3403 - 0,28 ° π   r a d 180 ° = 0,0223

Portanto:

n v i o l e t a = n v e r m e l h o + δ θ = 1,552 + 0,22 = 1,574

Logo, o ângulo de refração da luz violeta é n v i o l e t a = 1,574

Resposta

a )   δ θ = - t a n t a n   θ 2     δ n n   ,   b )   n v i o l e t a = 1,574

Ver Outros Exercícios desse livro