Um feixe de luz paralelo se propaga no ar e forma um ângulo de 47,5° com a superfície de uma placa de vidro que possui índice de refração igual a 1,66. (a) Qual é o ângulo entre a parte do feixe refletida e a superfície do vidro? (b) Qual é o ângulo entre a parte refratada e a superfície do vidro?
Passo 1
O que a gente tem que lembrar aqui é o seguinte: o ângulo de incidência e o ângulo de reflexão são iguais. Saca só:
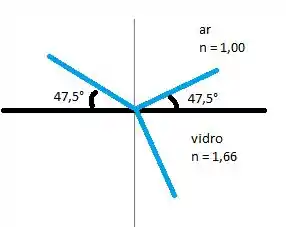
Então a resposta da letra a é: o ângulo entre a parte do feixe refletida e a superfície do vidro é
Passo 2
O que a gente tem que usar aqui é a lei de Snell, você lembra?
Mas olha, coisa importante: pra usar essa equação, os ângulos devem estar sendo medidos em relação a reta normal, beleza?
Então o nosso
Substituindo os valores, temos:
Colocando arcsen dos dois lados para acharmos o :
Lembrando que esse ângulo que a gente achou é o que tá relacionado com a normal, hein! Então pra achar o ângulo que o exercício realmente pede (que é o que esse feixe faz com a superfície de vidro), temos que fazer
E é essa a resposta da nossa letra b!