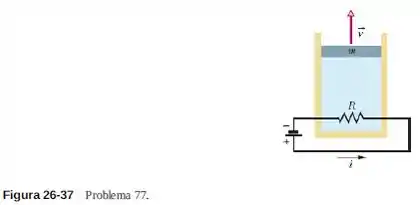
Na Fig. 26-37, um fio resistivo, ligado a uma bateria, é colocado no interior de um cilindro isolado termicamente, com um êmbolo sem atrito na extremidade superior, que contém um gás ideal. Uma corrente atravessa o fio, que tem uma resistência . Se a temperatura do gás permanece constante enquanto o êmbolo de se desloca para cima, qual é a velocidade limite do êmbolo?

Essa questão parece difícil, mas vou facilitá-la pra você! Saca só! A bateria não fornece uma força eletromotriz? Pois então, quando conectamos ela a uma resistência, essa vai fornecer uma potência que vai ser dissipada. Bom, mas o que isso tem a ver com o tal êmbolo? Essa potência dissipada pela resistência é que vai ser a energia (trabalho!!) responsável por deslocar o êmbolo para cima! Tenso né! Mas olha como fica tranquilo de resolver:

O é o trabalho realizado pela força peso para movimentar o êmbolo por, digamos, uma distância , e é o intervalo de tempo transcorrido. Por outro lado, a potência dissipada por um resistor é , então:

E o que tem a ver a velocidade? Aí que tá o pulo do gato! Velocidade não é distância percorrida por intervalo de tempo? No nosso caso então , certo? E é isso que temos ali na expressão de cima:

E daí podemos isolar a velocidade e deixar em função das outras variáveis:

Show!