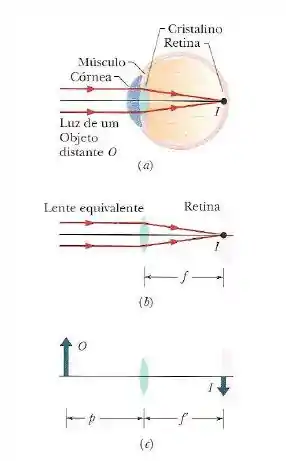
A Fig. 34-46a mostra a estrutura básica do olho humano. A luz é refratada pela córnea para o interior do olho e refratada novamente pelo cristalino, cuja forma (e, portanto, distância focal) é controlada por músculos. Para fins de análise, podemos substituir a córnea e o cristalino por uma única lente delgada equivalente (veja a Fig. 34-46b). O olho “normal” focaliza raios luminosos paralelos provenientes de um objeto distante O em um ponto da retina, no fundo do olho, onde começa o processamento do sinal visual. Quando o objeto se aproxima do olho, os músculos precisam mudar a forma do cristalino para que os raios formem uma imagem invertida do objeto na retina (Fig. 34-46c). (a) Suponha que, no caso de um objeto distante, como nas Figs. 34-46a e 34-46b, a distância focal f da lente equivalente do olho seja 2,50 cm. Para um objeto a uma distância p = 40,0 cm do olho, qual deve ser a distância focal f′ da lente equivalente para que o objeto seja visto com nitidez? (b) Os músculos do olho devem aumentar ou diminuir a curvatura do cristalino para que a distância focal se torne f′?

Faaala galera, bora pra mais uma questãzinha do nosso livro!

Para o item a) temos os seguintes passos:

Quando o olho está relaxado, seu cristalino focaliza objetos distantes na retina, a uma distância atrás da lente. Iremos definir na equação das lentes para que assim obtermos:

Onde é a a distância focal da lente. Tudo tranquilão né? Bora continuar!

Com a relação acima a gente tem que , quando o olho focaliza objeto mais próximos a distância da imagem continua a mesma, porém a distância do objeto e a distância focal mudam de comprimento. Se é a nova distância do objeto e é a nova distância focal, a gente tem que:

Se liga que no passo anterior temos que , então substituindo na expressão acima para descobrir o valor de , ficamos com:

Substituindo pelos valores dados no enunciado do item a) temos:

Tudo certinho, agora vem comigo pro item b)!