Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 35.Problemas Adicionais - Ex. 84
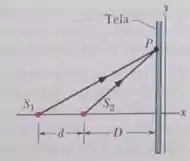
Na Fig. 35-49, duas fontes pontuais isotrópicas e emitem luz em fase com a mesma amplitude e comprimento de onda . As fontes estão no eixo , separadas por uma distância . Uma tela de observação paralela ao plano está situada a uma distância de . A figura mostra dois raios chegando ao ponto da tela, situado a uma altura . (a) Para que valor de os raios representam a menor diferença de fase possível? (b) Que múltiplo de representa a menor diferença de fase possível? (c) Para que valor de os raios apresentam a maior diferença de fase possível? Que múltiplo de representa (d) a maior diferença de fase possível e (e) a diferença de fase para ? (f) Para , a intensidade no ponto é máxima, mínima, mais próxima do máximo ou mais próxima do mínimo?
Passo 1
O exercício diz que duas fontes e emitem luz com comprimento de onda . Queremos estudar a figura de interferência no ponto da tela.
A distância de até será
Já a distância de até será
Assim, a dirença de caminho dos dois raios de luz é
A condição de interferência é
Se for par ela será construtiva e se for ímpar ela será destrutiva! A diferença de fase, em múltiplos de comprimento de onda é .
Passo 2
A menor diferença de fase possível ocorre para . Nesse caso,
Isso só é possível se . Nesse caso, a diferença de fase em múltiplos de comprimento de onda é .
Passo 3
A maior diferença de fases ocorre quando . Nesse caso,
Portanto,
Assim, a maior diferença de fase, em múltiplos de comprimento de onda, é .
Passo 4
Se :
Assim,
Portanto, a diferença de fase em múltiplos de comprimento de onda é . Assim,
Como é mais próximo de um número par que um número ímpar, está mais próximo de um máximo de interferência!