Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 42.3 - Ex. 44
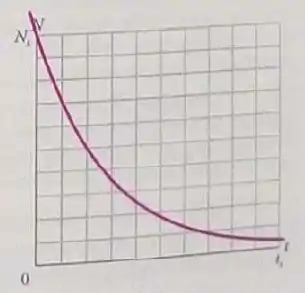
A figura 42-19 mostra o decaimento de uma amostra radioativa. A escala dos eixos é definida por e . Qual é a atividade da amostra no instante ?
Passo 1
De acordo com o gráfico do enunciado, o número de átomos no instante era .
E o número caiu pela metade no instante .
Desta forma podemos utilizar a equação:
para encontrar quanto vale a constante de desintegração .
Passo 2
Vamos aplicar o logaritimo natural em ambos os lados da equação e isolar , desta forma obtemos:
Utilizando os dados que analizamos do gráfico no passo 1, para calcular :
Passo 3
Agora podemos facilmente calcular facilmente qual será a atividade da amostra no instante . Para isso vamos primeiramente calcular o valor de , nesse instante.
Portanto a atividade será:
Resposta
Ei, a resposta está no passo a passo :)