A fim de forçar um dos dentes incisivos para alinhamento com os outros dentes da arcada,
um elástico foi amarrado a dois molares, um de cada lado, passando pelo dente incisivo , como mostra a Figura G .1 .8 . Se a tensão no elástico for 12 N, quais serão a intensidade e a direção da forca aplicada ao dente incisivo?
Passo 1
Primeiramente vamos fazer o diagrama de corpo livre, para esquematizar todas as forças, e como elas atuam no dente:
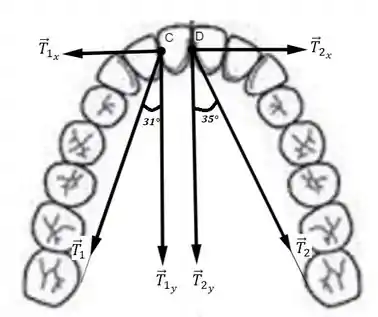
Com o DCL esquematizado, podemos analisar as forças atuantes no dente, e então deduzir as condições possíveis para a solução do problema:
Passo 2
Podemos usar a definição de força resultante:
Sempre p/ direita, p/ esquerda:
A direção da força , é dado por:
Passo 3
Vamos começar pela horizontal:
Sabemos que: O problema forneceu a tensão no elástico,
Como o elástico é um só,
Passo 4
Vamos agora para a vertical:
Sabemos que:
Passo 5
As componentes da força resultante são:
Módulo de :
Direção de :
Resposta