Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 31.Exercícios e Problemas - Ex. 60
Um fio de alumínio consiste de três segmentos, como mostrado na FIGURA P31.60 . A corrente no segmento superior é de 10 A. Em, cada um dos segmentos, determine
a. A corrente I.
b. A densidade de corrente J.
c. A intensidade do campo elétrico E.
d. A velocidade de deriva .
e. O tempo médio entre colisões sucessivas .
f. A corrente de elétrons i.
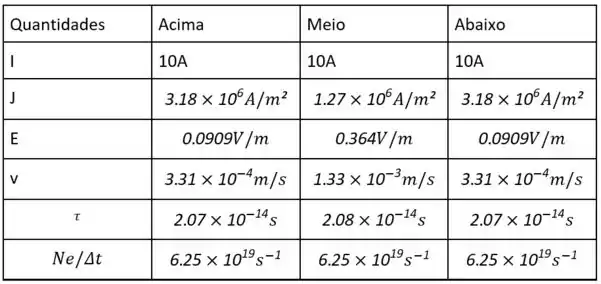
Disponha seus resultados em uma tabela para melhor visualização.
Passo 1
Fala galera, tudo tranquilo? Nesse problema é um item puxando o outro. Recomendo pegar valor da condutividade do alumínio na tabela do livro. Para começar temos 3 cilindros. O cilindro acima e abaixo tem a mesma medida e o cilindro no meio, tem medida diferente.
A corrente é conservada logo, é a mesma corrente nos 3 fios, ou seja
A densidade de corrente é
A intensidade do campo elétrico é dada por
Passo 2
A velocidade de deriva é dada pela equação , onde é a densidade eletrônica do alumínio.
O tempo médio entre as colisões é dado pela equação 31.7
Para a corrente de elétrons i, temos a equação
que é a corrente dividida por 1 elétron, então se temos uma corrente de 10A, ficamos com:, Como há conservação da corrente, este valor é o mesmo para os 3 cilindros.
Resposta
(a)
(b)
(c)
(d)
(e)
(f)
