Um fio retilíneo muito longo (trate como infinito) está eletrizado com uma densidade linear de carga λ . Calcule a força com que atua sobre uma carga puntiforme q colocada à distância ρ do fio. Sugestão: tome a origem em O (fig.) e o fio como eixo z. Exprima a contribuição de um elemento dz fio à uma distância z da origem em função do ângulo θ da figura. Use argumentos de simetria.

Deste modo nossa resposta é: F → = qλρ 2 π ϵ 0∫ 0 L d z ( ρ ² + z ² ) 3 / 2 = qλρ 2 π ϵ 0 z ρ ² ( ρ ² + z ² ) 1 / 2 | 0 L = qλ2 π ϵ 0ρL ( ρ ² + L ² ) 1 / 2 - 0 ² ² ² ² ² ² ² colocando L em evidência F → = qλ2 π ϵ 0ρ1 ( ρ ² / L ² + 1 ) 1 / 2 ² ² , para L → ∞ (fio muito longo) a força eletrostática toma a forma simplificada: F → = qλ2 πϵ 0ρ .

Enunciado

Física - Moysés - Vol. 3- Ed: 2º - Capítulo 2.Problemas - Ex. 8

Um fio retilíneo muito longo (trate como infinito) está eletrizado com uma densidade linear de carga . Calcule a força com que atua sobre uma carga puntiforme q colocada à distância do fio. Sugestão: tome a origem em O (fig.) e o fio como eixo z. Exprima a contribuição de um elemento dz fio à uma distância z da origem em função do ângulo da figura. Use argumentos de simetria.

Passo 1

Fala galera, tudo tranquilo? Quando ele sugere usar argumentos de simetria, é fazermos uma espécie de espelhamento, como mostrarei na figura abaixo:

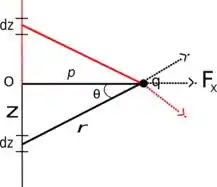
A parte em vermelho é nosso “argumento de simetria”. Na componente X temos o versos î com , perceba que são duas componentes da força partindo de dz em ambos os lados acima e abaixo da nossa imagem.

Como se trata de uma densidade linear de carga. Nosso dQ(carga de um elemento dz do fio) passa a ser da forma Se olharmos acima e abaixo, na componente x temos duas contribuições de dz. Portanto podemos tratar da seguinte forma

Integrando ambos os lados ficamos com

Passo 2

Bem, nosso próximo passo é ir atrás da solução da nossa integral. Essa integral é do tipo trigonométrica onde podemos obter a solução dela em uma tabela de integrais a qual nosso resultado passa a ser:

Resposta

Deste modo nossa resposta é:

colocando L em evidência

, para (fio muito longo) a força eletrostática toma a forma simplificada: