Um foguete move-se ao longo de uma órbita elíptica em torno da Terra. Para adquirir a EC necessária para escapar, usando uma dada quantidade de combustível, ele deveria acionar seus motores no apogeu ou no perigeu? (Dica: deixe a fórmula orientar seu pensamento. Suponha que o empuxo F seja breve e tenha a mesma duração em qualquer caso. Então considere a distância d que o foguete percorreria durante esse breve acionamento no apogeu e no perigeu.)

Como , o lugar da trajetória que possibilita a realização do menor trabalho possível, é aquele tal que é o menor possível.

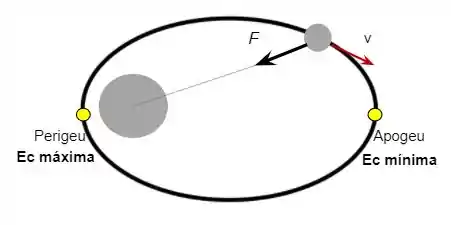
Vemos então que se o foguete escapar no perigeu, onde a do satélite é máxima na trajetória, será o menor possível. Consequentemente, o trabalho também será o menor possível, e será gasto a menor quantidade de combustível no processo de escape.