Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 30.Exercícios e Problemas - Ex. 67
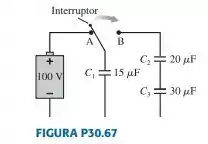
Inicialmente, o interruptor da FIGURA P30.67 está na posição A, e os capacitores , descarregados. Então, o interruptor é movido para a posição B. Logo após, qual é a carga e qual é a diferença de potencial através de cada capacitor?
Passo 1
Faaaaaala, galera... Tranquileba??
Bom, quando o interruptor é ligado em B, não há uma bateria que forneça energia. Assim, toda a energia do sistema será aquele que o capacitor fornecer. Assim, a quantidade de carga é:
E essa será a carga que será distribuída quando o interruptor for passado pra B.
Passo 2
Após a chave ser movida, a carga é redistribuída, sendo assim vai pra e para . Tomando a equação anteriormente dita, podemos relacionar a voltage através desses capacitores:
Postos os capacitores e em série, logo podemos aplicar a lei para os capacitores em série:
Assim:
E retornando:
E sendo os capacitores combinados em série,
Passo 3
Assim:
A bateria distribui 100V e o capacitor 111V, interessante, não?!