Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 10º - Capítulo 8.Problemas - Ex. 82

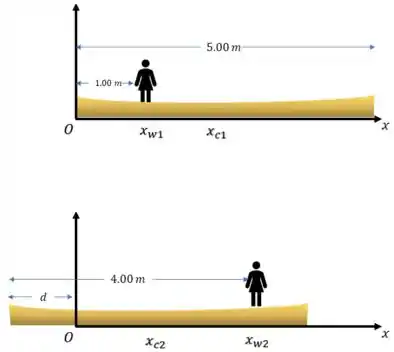
Uma jovem de 45,0 kg está em pé sobre uma canoa de 60,0 kg e comprimento igual a 5,00 m . Ela caminha a partir de um ponto situado a 1,00 m de uma das extremidades da canoa até atingir a outra extremidade da canoa ( Figura 8.42 ) . Desprezando a resistência da água ao movimento da canoa , qual a distância que a canoa se move nesse processo?

Passo 1

Beleza pessoal?! Espero que esteja tudo bem com meu os herdeiros de Newton. Vamos dar início a mais uma resolução com o padrão de qualidade do Responde aí, então pegue seu lápis, caderno e café e vamos nessa!!!

Tomamos a origem na posição inicial da extremidade esquerda da canoa e +x para a direita, então a coordenada x da posição inicial da mulher é x w 1 = 1.00   m .

Sabemos que, se um objeto homogêneo tem um centro geométrico, é aí que se encontra o centro de massa; Portanto, a coordenada x do centro de massa da canoa é x c 1 = l / 2 = 2.50 m .

Agora, aplicamos a equação (1), ao sistema da mulher e da canoa, assim obtemos:

X c m , 1 = m w x w 1 + m c x c 1 m w + m c

X c m , 1 = ( 45.0 ∙ 1 ) + ( 60.0 ∙ 2.5 ) 45.0 + 60.0 = 1.86   m

Passo 2

Como a mulher se move para a direita, a canoa se move para a esquerda; Então, se a canoa percorre uma distância d, a posição final da mulher e da canoa é:

x w 2 = ( 5.00 - 1.00 ) - d = 4.00 - d

x c 2 = 2.50 - d

X c m , 2 = m w x w 2 + m c x c 2 m w + m c

= 45 ( 4 - d ) + 60 ( 2.5 - d ) 45 + 60

= 330 - 105 d 105

Passo 3

Como não há força externa resultante no sistema, o momento total é conservado (Δp=∑F⋅t).

Mas a canoa estava inicialmente em repouso, então o momento total é zero ;

Portanto a velocidade do centro de massa é zero, isso significa que ele permanece em repouso e assim temos:

X c m , 1 = X c m , 2

1.86 = 330 - 105 d 105

330 - 105 d = 195

d = 330 - 195 105 = 1.29   m

Resposta

1.29   m para a esquerda