Um menino deseja deslocar uma tora de madeira sobre o chão puxando uma corda amarrada
a ela, como indica a Figura G .1 .2 . Sabendo-se que o coeficiente de atrito estático entre a madeira e a terra vale e que a massa da tora é de , com que forca o menino deve puxar a corda para deslocar a tora se a direção da corda forma , em relação a horizontal, um angulo de 5°?
Passo 1
Primeiro desenhamos um diagrama de corpo livre (DCL), esquematizando todas as forças que agem sobre a tora, com isso facilita o desenvolvimento das equações, para a solução do exercício .
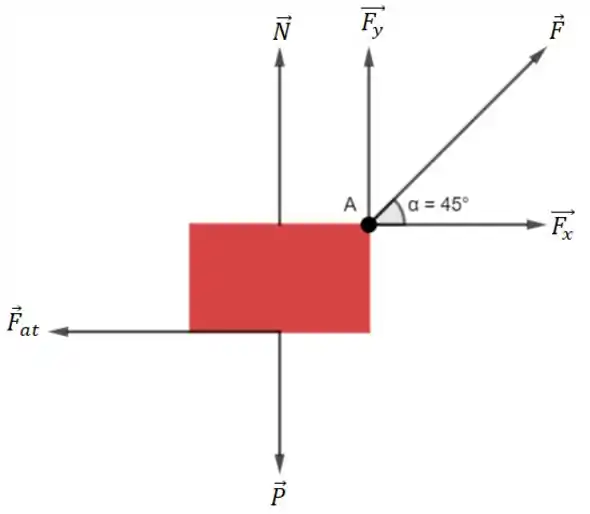
Considere a tora, o bloco vermelho:
Passo 2
Para a tora se movimentar
Na horizontal:
Onde:
subst. em
Passo 3
Mas:
Onde:
subst. em
Passo 4
Onde:
,
Subst. em
Passo 5
Fazendo a distributiva, temos:
Colocando em evidência:
Subst. os valores numéricos:
Resposta