Uma onda progressiva transversal numa corda longa é descrita pela equação
Sendo dado em , em e em . Desenhe a configuração da corda até para os instantes e . Determine a amplitude, a velocidade, o período e a frequência da onda.
Passo 1
E aíiíí cara! Vamos pra mais uma de ondas
Temos a equação de onda:
Mas pera pera pera, antes de qualquer coisa, vamos ajustar essa equação. Pra isso, vamos transformar o em radianos. Sabemos que , certo? Então:
Agora sim ficou mais simples de compararmos essa equação com a equação geral de onda:
Comparando, já temos:
Vamos lá responder as perguntas
Passo 2
Antes de tudinho, vamos encontrar a frequência e o período da onda. Sabemos que
Mas vimos lá no passo 1 que , então:
Dessa forma, o nosso período é:
Passo 3
Agora vamos encontrar o comprimento de onda e a velocidade
No passo 1, vimos que , mas sabemos que:
Então
Mas sabemos que
Então
Fechou, encontramos nossas principais informações sobre essa ondinha

Passo 4
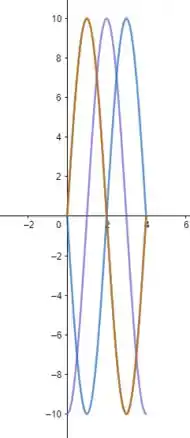
Queremos desenhar a onda até para os instantes e
Como , então queremos desenhar para
Pera, vamos entender melhor: essa onda está se movendo com velocidade de , então quando o tempo vai mudando, a configuração da onda também vai mudando, sacou? E aí vamos desenhar essa configuração pra 4 valores diferentes de tempo. Bora lá!
Então, para vamos ter uma onda de amplitude e tal que as intersecções com os eixos são:
Então, em , a onda só vai ter para valores pares de , assim:

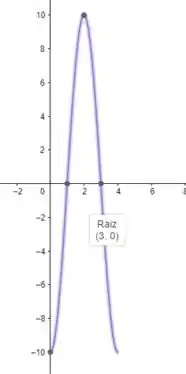
Passo 5
Então, para vamos ter uma onda de amplitude e tal que as intersecções com os eixos são:
Então, em , a onda só vai ter para valores ímpares de , assim: (repara que só deslocamos a onda do passo anterior em para a direita)
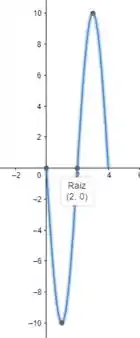
Passo 6
Então, para vamos ter uma onda de amplitude e tal que as intersecções com os eixos são:
Então, em , a onda só vai ter para valores pares de , assim: (repara que só deslocamos a onda do passo anterior para a direita)
(como é metade do nosso período, a onda vai ser igual a de mas ao contrário)
Passo 7
Então, para vamos ter uma onda de amplitude e tal que as intersecções com os eixos são:
Então, em , a onda só vai ter para valores pares de , assim: (repara que só deslocamos a onda do passo anterior para a direita)
(como é nosso período, a onda vai ser igual a de )
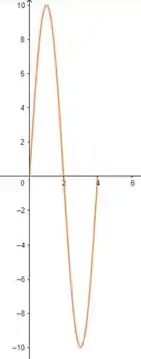
Resposta