Enunciado
Física - Moysés - Vol. 3- Ed: 2º - Capítulo 2.Problemas - Ex. 9
Uma partícula está a uma distância de massa “m” e carga negativa -q está vinculada a mover-se sobre a mediatriz que ligam duas cargas positivas +Q, separadas por uma distância d (como mostra figura do livro). Inicialmente, a partícula Y
Passo 1
Fala galerinha, beleza? Vamos começar examinando um esquema dessas cargas como mostra a figura abaixo.
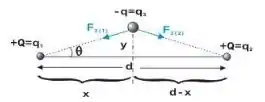
Sabemos que temos duas cargas + e uma carga -. As decomposições das formas são dadas pelas forças em X. Vamos igualar as forças e ficar atento as distâncias x e d-x que iremos utilizar devido as forças e suas interações com a carga -q
vamos voltar nos olhos apenas apenas com os termos relacionados a distância:
com isso teremos as soluções desta equação
Passo 2
A componente em Y, que atendem o sentido da vertical, é da forma . O valor 2 ocorre pelo fato das duas cargas Q estarem exercendo força na carga -q no mesmo sentido (para cima). Para o caso do seno, temos
onde lembre-se que . O que nos dá a seguinte equação para a componente em Y.
. As condições nos mostram que o Denominador não pode ser zero, e a força não pode ser zero, entretanto, Y pode ser bem próximo de zero. Observe que a componente da força em Y existe para que a partícula não “caia” do oscilador. Ela atua como uma força restauradora, fazendo com que a carga execute movimento para cima e para baixo. Quando está na amplitude máxima, a força age puxando a partícula para que ela execute o mesmo movimento em sentido oposto. Se você estiver bem atento até aqui, esse movimento de subir e descer, é um movimento de MHS. Nossas equações fica na forma:
Resposta
Agora vamos diminuir essa equação para facilitar nosso trabalho.
onde ,
A equação para um oscilador é:
, comparando as forças temos:
Para pequenas oscilações ou deslocamentos muito pequenos, Y
para y
.
Para a frequência angular , teremos a equação na forma:
como queriamos mostrar.