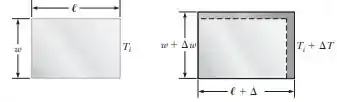
A placa retangular mostrada na Figura P16.60 tem uma área , igual a . Se a temperatura aumentar em , cada dimensão aumenta de acordo com a Equação 16.4, onde a é o coeficiente médio de expansão linear. (a) Mostre que o aumento em área é . (b) Que aproximação essa expressão assume?
Passo 1
Falaaa galerinha, tudo bem?
Bora pra mais um?
- A variação da área pode ser escrita como a diferença da área final pela inicial. Portanto:
- Para encontrarmos essa aproximação, consideramos que:
Como em termos de dilatação os valores de são muitos pequenos com relação às medidas , podemos desprezar o produto entre eles:
Passo 2
A variação do comprimento linear é dada por:
Substituindo, teremos:
Passo 3
Como visto anteriormente, a expressão:
Passo 2
Portanto:
Com isso, concluímos que a consideração inicial de desprezar o termo do produto de está correta.
Resposta
Vide a explicação.