Quais são as propriedades de dois vetores a e b tais que
(a) a + b = c ea + b = c;
(b) a + b = a – b;
(c) a + b = cea² + b² = c²?
Passo 1
Fala aí! Bora começar relembrando um conceito aqui: a regra do polígono.
Bom, a regra do polígono nos diz que, para somarmos vetores graficamente, juntamos os vetores pela extremidade do primeiro e origem do segundo e traçamos uma linha da origem do primeiro para a extremidade do último vetor, essa linha será a resultante.
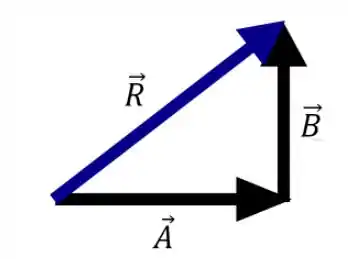
No exemplo acima, a resultante é encontrada da seguinte forma:
E como fazemos para encontrar o módulo de ? Então, no exemplo anterior, bastaria aplicar o Teorema de Pitágoras, mas isso não é válido quando os vetores e não formarem um ângulo de 90º, então vamos ter que aplicar a lei dos cossenos, que é expressa assim:
Perceba que a equação é bem semelhante à de Pitágoras, que nada mais é do que um caso particular em que vale 90º, cujo cosseno anula o último termo!
Bom, dito tudo isso, vamos ver como isso vai ser relevante agora. Vamos começar aplicando essa lei para o caso em que os vetores são paralelos:
Vou reorganizar os termos pra você perceber uma coisa.
“O quadrado do primeiro mais duas vezes o primeiro vezes o segundo mais o quadrado do segundo”! Vamos remontar esse produto notável:
Agora, como temos os dois lados elevados ao quadrado, podemos cancelar os expoentes. Aí chegamos em:
Tá aí! Encontramos que a soma vetorial de dois vetores será igual à sua soma escalar quando esses vetores forem paralelos!
Passo 2
Para a próxima, não vamos precisar fazer contas, mas temos que usar um pouquinho de raciocínio. Nos foi perguntado quando que um vetor , se somado a ele um vetor , será igual a ele mesmo após subtraído o tal vetor . Perceba que isso só é possível em dois casos: ou é igual a zero, ou ambos os vetores são iguais a zero!
Passo 3
Beleza, agora que passamos por tudo isso, se você entendeu bem o primeiro passo, tenho certeza de que vai sacar essa aqui rapidinho. Lembra quando citei o Teorema de Pitágoras e o comparei com a lei dos cossenos? Então, isso é exatamente o que precisamos aqui!
Se liga, se os vetores forem perpendiculares, tal como na imagem lá no passo 1, a expressão fica assim:
Como o cosseno de 90º é zero, todo aquele último termo é anulado. Aí ficamos com:
Que é exatamente a condição pedida pelo enunciado
Resposta
(a) e são paralelos.
(b) .
(c) e são perpendiculares.