Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 10º - Capítulo 1.Questões para discussão - Ex. 17

Seja A → um vetor diferente de zero. Por que A → / A é um vetor unitário e qual a sua direção? Seja θ o ângulo entre A → e o eixo O x , explique por que ( A → / A ) ⋅ î é denominado co-seno diretor deste eixo

Passo 1

Olá pessoal, bora para mais uma questãozinha?

O problema nos dá um vetor genérico, então seja A → = a x , a y , a z o nosso vetor, vamos calcular seu módulo (A), assim temos:

A = a x 2 + a y 2 + a z 2

Assim quando fazemos A → / A temos que:

A → A = a x , a y , a z a x 2 + a y 2 + a z 2 = [ a x a x 2 + a y 2 + a z 2 , a y a x 2 + a y 2 + a z 2 , a z a x 2 + a y 2 + a z 2 ]

Para facilitar chamaremos A → A = B → .

Passo 2

Agora para verificar se B → é realmente um vetor unitário, calcularemos o seu módulo, ou seja:

B = a x 2 a x 2 + a y 2 + a z 2 + a y 2 a x 2 + a y 2 + a z 2 + a z 2 a x 2 + a y 2 + a z 2 = a x 2 + a y 2 + a z 2 a x 2 + a y 2 + a z 2 = 1 = 1

Logo foi possível demonstrar que A → / A é de fato um vetor unitário.

A direção do vetor continuará a mesma, pois se multiplicarmos o vetor por uma constante (1/A), isso não irá mudar a sua direção.

Passo 3

Agora faremos uma ilustração para demonstrar a segunda parte do problema.

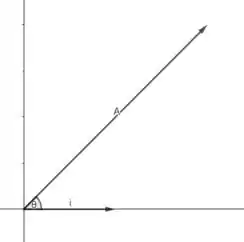
Temos que

A → A ⋅ î = a x , a y A ⋅ 1,0 = a x A

Assim encontramos a componente x do vetor dividida pelo módulo do vetor.

Agora comparando com o cosseno diretores de um vetor, temo que:

c o s θ = b → ⋅ î b ⋅ i = b x b

Desta forma podemos concluir que a expressão ( A → / A ) ⋅ î é uma forma de calcular o cosseno diretor do ângulo em relação ao vetor e o eixo Ox.

Finalmente finalizamos mais uma questão. Te vejo na próxima!!

Resposta

Foi provado que um vetor ( A → / A ) tem módulo igual a 1 e foi provado que o cosseno diretor do ângulo entre o vetor e o eixo x é dado por ( a X → / A ).