Com um simples diagrama, mostre que, quando um espelho no qual incide um feixe luminoso fixo é girado por um determinado ângulo, o feixe refletido gira no dobro deste ângulo. (Este valor duplicado do deslocamento angular do feixe torna mais evidentes as irregularidades existentes no vidro ordinário de janelas.)

Quando um raio incide em um ângulo, já sabemos pela lei da reflexão que esse ângulo é o mesmo que o ângulo que o raio é refletido. Se o espelho for girado por um ângulo, vamos aumentar o ângulo de incidência, que vai ser o mesmo de reflexão, e como temos ele duas vezes, esse ângulo vai ser dobrado. Se não entendeu ainda, fica tranquilo que vai ficar mais claro depois do desenho.

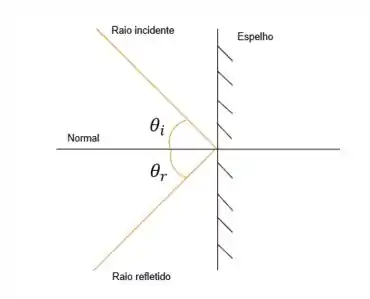
Primeiro vamos ver o caso inicial com o espelho sem nenhum giro. Fica assim:

Como sabemos, pela lei da reflexão, o , que é o ângulo de incidência do raio que está chegando é igual ao que é o ângulo de reflexão do raio que sai do espelho.

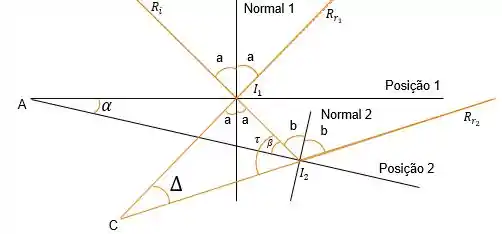
Agora fazendo uma rotação de um ângulo teremos a figura

Onde temos que a posição 1 é onde o espelho estava no início e a posição 2 é depois da rotação. Agora vamos aos termos pra entenderem tudo.

é o raio incidente,

é o raio refletido na posição 1 do espelho,

é o raio refletido na posição 2 do espelho,

é a ponto no espelho que o raio incidente acerta o espelho na posição 1,

é a ponto no espelho que o raio incidente acerta o espelho na posição 2,

é o ângulo que o espelho foi girado,

é o ângulo que o raio refletido gira com o giro do espelho,

a é o ângulo de incidência e reflexão na posição 1 do espelho (pela lei da reflexão, os dois são iguais),

b é o ângulo de incidência e reflexão na posição 2 do espelho,

é o ângulo para completar o ângulo entre a normal e o espelho na posição 2,

é o ângulo entre o raio incidente e o prolongamento do raio refletido na posição 2 do espelho.

Agora que entendemos o que cada coisa, podemos ir aos cálculos.

Primeiro, vendo o triângulo temos

Pela soma dos ângulos internos de um triângulo ser .

Mas sabemos que, se olharmos a reta do raio refletido 2, vamos ter

E assim

Substituindo a equação (2) na equação (1) vamos ter

Agora vamos olhar pro triângulo tendo

Onde esse foi tirado do fato que o ângulo que falta pra completar o terceiro ângulo no ponto é oposto pelo vértice e, portanto, igual ao ângulo que falta pra completar o ângulo entre a normal 1 e a posição 1 do espelho. Como o ângulo entre a normal 1 e a posição 1 do espelho é temos que o que falta é .

O ângulo é o ângulo que falta entre a posição 2 do espelho e a normal 2, que também é . Então o que falta pra completar é . Assim

Substituindo a equação (5) em (4) ficamos com

Substituindo a equação (6) na equação (3) teremos

Provando que o raio é desviado duas vezes o ângulo de rotação do espelho.