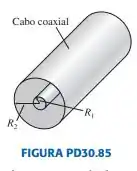
Sinais de alta freqüência geralmente são transmitidos ao longo de cabos coaxiais, tal como o que é mostrado na FIGURA PD30.85. Por exemplo, o cabo ao qual está conectada a sua TV por assinatura é um cabo coaxial. O sinal é conduzido sobre um fio de raio , enquanto o condutor externo, de raio , está aterrado (ou seja, com ). Um material isolante preenche o espaço entre os dois condutores, e um isolante plástico recobre totalmente o exterior do cabo.

1. Obtenha uma expressão para a capacitância por metro do cabo coaxial. Considere que o material isolante entre os cilindros seja o ar.
2. Determine o valor da capacitância por metro do cabo se e .

Faaaaaala, galera... Tranquileba??

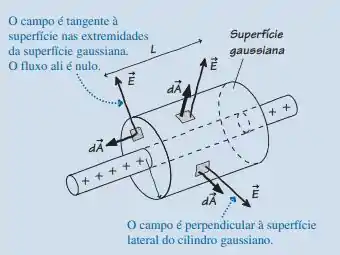
Dado que o campo é perpendicular a superfície e tomando a simetria do sistema podemos aplica a lei de Gauss para o fluxo Elétrico:

Sendo o campo constante em todo o fio, logo:

E a área gaussiana do cilindro é dada como:

E a densidade linear de carga é:

Assim ficando:

E assim, a relação entre a diferença de potencial e o campo elétrico é:

Assim:

É pedido pra gente calcular a ddp entre os dois cilindros, assim . De modo que

Lembrando que: