Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 30.Exercícios e Problemas - Ex. 44

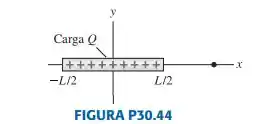
  1. Use os métodos do Capítulo 29 para determinar o potencial a uma distância x sobre o eixo perpendicular ao bastão carregado da FIGURA P30.44.
  2. Use o resultado do item anterior para determinar o campo elétrico a uma distância x sobre o eixo do bastão

Passo 1

Faaaaaala, galera... Tranquileba??

Sabemos por definição que:

V = 1 4 π ε 0 q d

Assim para qualquer ponto

V b a s t ã o = 1 4 π ε 0 Δ q r i

Sabe-se que:

Δ q Δ x = Q L

Logo:

V b a s t ã o = 1 4 π ε 0 Q   Δ x L r i

E:

r i = x 0 - x i

Para uma posição qualquer.

Assim:

V b a s t ã o = 1 4 π ε 0 Q   Δ x L x 0 - x i

Seja o ponto P colocado a uma distancia x 0 da origem, então façamos x i = x sendo x uma distancia o centro.

Assim:

V b a s t ã o = 1 4 π ε 0 Q   Δ x L x 0 - x

E integrando, veja que - L 2 ≤ x ≤ + L 2  

Portanto:

V b a s t ã o = Q 4 π ε 0 L ∫ - L 2 L 2 d x x 0 - x

Passo 2

Façamos:

u = x 0 - x

Logo:

d u = - d x

Assim:

V b a s t ã o = Q 4 π ε 0 L ∫ - d u u = V b a s t ã o = - Q 4 π ε 0 L ln ⁡ u

Retornando u = x 0 - x e os limites de integração:

V b a s t ã o = - Q 4 π ε 0 L ln ⁡ x 0 - x - L 2 L 2 = Q 4 π ε 0 L ln ⁡ x 0 + L 2 x 0 - L 2

Assim retornando a x 0 = x

V b a s t ã o = Q 4 π ε 0 L ln ⁡ x + L 2 x - L 2

Passo 3

Para b)

Sabendo que E → = - ∇     V →

Assim:

E → = d d x Q 4 π ε 0 L ln ⁡ x + L 2 x - L 2 =

= -   Q 4 π ε 0 L 1 x + L 2 - 1 x - L 2 = Q 4 π ε 0 1 x 2 - L 2 2

Portanto

E → = Q 4 π ε 0 1 x 2 - L 2 2

Resposta

  1. V b a s t ã o = Q 4 π ε 0 L ln ⁡ x + L 2 x - L 2

E → = Q 4 π ε 0 1 x 2 - L 2 2

Ver Outros Exercícios desse livro