a) Se o coeficiente de atrito cinético entre os pneus e um pavimento seco for de , qual é a menor distância para fazer um carro parar bloqueando o freio, quando o carro se desloca a ? b) Sobre um pavimento molhado, o coeficiente de atrito cinético se reduz a . A que velocidade você poderia dirigir no pavimento molhado para que o carro parasse na mesma distância calculada em (a)? (Nota: Bloquear os freios não é a maneira mais segura de parar.)
Passo 1
Olá, galerinha! Tudo bom? Bom, aqui nós temos um carro se deslocando em um sentido e ao acionar o freio, teremos uma força de atrito no sentido contrario parando o carro.
Nós queremos encontrar (a) a menor distância para fazer o carro parar e (b) a velocidade que se poderia dirigir no pavimento molhado com um coeficiente de atrito cinético .
Para resolver essa questão, nós vamos aplicar a 2º lei de Newton, para encontrar a aceleração que pode ser dada ao carro pela força de atrito cinético.
Em seguida precisamos usar uma equação de aceleração constante.
Vamos tomar nosso referencial como na direção em que o carro está se movendo. Com isso o diagrama de corpo livre fica assim:
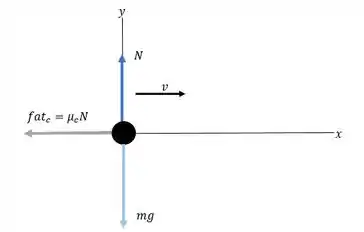
Então, o que nós vamos fazer é calcular o somatório dessas forças de acordo com a segunda lei e depois usar a equação de Torricelli () para descobrir o deslocamento e a velocidade inicial na segunda situação. Vamos lá!
Passo 2
a) Como estamos buscando o deslocamento, só vamos tratar as forças no eixo .
Para o :
Somando as forças atuantes:
E isolando a aceleração, temos:
Passo 3
Pelo enunciado nós temos as seguintes informações:
Como não temos o tempo, vamos usar a equação de Torricelli:
Assim, admitindo que ele parte do repouso, temos :
E isolando na equação:
Substituindo encontrado no passo anterior:
E substituindo os valores, temos:
Encontramos o deslocamento.
Passo 4
b) Agora precisamos de um novo para um pavimento molhado, sabendo que seu coeficiente de atrito cinético se reduz a .
Ainda utilizando Torricelli, uma vez que encontramos , vamos ter:
E substituindo os valores, temos:
Prontinho, galera! Até a próxima! 😉