Com uma vareta e barbantes, construa um “traçador de trajetória” como o que é mostrado na página 187.
Passo 1
E aí, galera! Tudo tranquilo? Você deve se lembrar que a primeira lei de Kepler estabelece que os planetas descrevem órbitas elípticas com o sol num dos focos. Mas o que é uma elipse (referente a órbita elíptica)?
A elipse é uma figura geométrica que tem como principal propriedade a constância entre a soma das distâncias de qualquer ponto aos dois focos. Matematicamente:
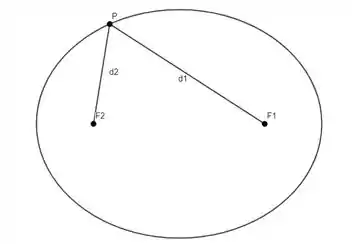
Vamos utilizar esse conhecimento para construir um “traçador de trajetória” e desenhar uma elipse.
Passo 2
Para realizar o que foi proposto devemos seguir alguns passos:
1°) Para construir o “traçador de trajetória é simples”, pegue um barbante e amarre suas extremidades em duas varetas. (Esse passo já resolve o que foi pedido no enunciado. Mas vamos além disso! Vamos utilizar o nosso “traçador”.
2°) Agora, apoie as duas varetas verticalmente em cima de dois pontos fixos. Esses pontos serão os focos de nossa elipse.
3°) Então, encoste o lápis no barbante até que não haja folga entre eles.
4°) Para enfim desenhar a elipse, deslize o lápis através do barbante até completar uma volta completa. Pronto, agora você tem uma elipse!
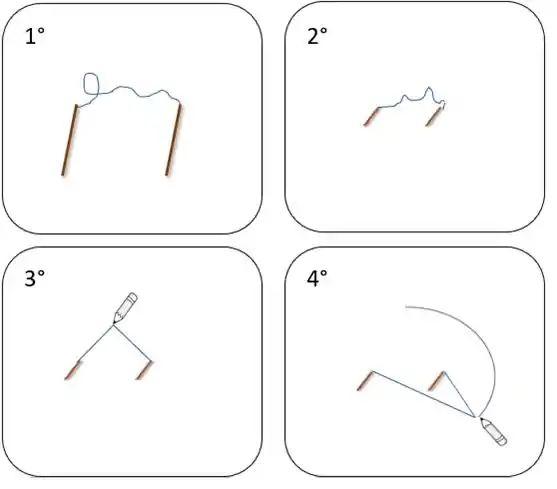
Obs: A quarta imagem representa apenas um momento do processo que deve ser feito no quarto passo.
Passo 3
Perceba que em qualquer ponto da quarta etapa o tamanho do barbante se mantém inalterado, ou seja, a soma das distâncias da ponta da caneta a ponta das varetas é constante. Acabamos de usar uma propriedade matemática para desenhar a elipse!
Resposta
Ei, a resposta está no passo a passo :)