Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 10º - Capítulo 3.Exercícios - Ex. 6

A velocidade de um cachorro correndo em um campo aberto possui componentes v x = 2,6 m s ,   v y = - 1,8 m s para t 1 = 10 s . Para o intervalo de tempo entre t 1 = 10 s   e   t 2 = 20 s , a aceleração média do cachorro possui módulo igual a 0,45m/s², formando um ângulo de 31 ° médio considerando uma rotação do eixo + O x para o eixo + O y . Para t 2 = 20 s ,

  1. Quais são os componentes x e y da velocidade do cachorro?
  2. Ache o módulo, a direção e o sentido da velocidade do cachorro.
  3. Faça um desenho mostrando o vetor velocidade para t 1 e   p a r a   t 2 . Qual é a diferença entre estes vetores

Passo 1

Olá pessoal, bora para mais uma!?

Primeiramente temos que encontrar as componentes da aceleração do cachorro, assim sendo:

a x = 0.45 m s 2 * c o s 31 ° = 0.39 m / s ²

a y = 0.45 m s 2 * s e n 31 ° = 0.23 m / s ²

Com isso conseguimos obter as componentes x e y da velocidade do cachorro no intervalo t 2 = 20 s .

a x = d v x d t

a x = ( v x f - v x i ) d t  

v x f =   a x d t + v x i

Assim substituindo os valores temos que:

v x f =   a x d t + v x i

v x f = 0.39 m s 2 * 10 s + 2.6 m s = 3.9 m s + 2.6 m s = 6.5 m / s

Para v y f é o mesmo procedimento, assim temos:

v y f =   a y d t + v y i

v y f = 0.23 m s 2 * 10 s - 1.8 m s = 2.3 m s - 1.8 m s = 5 m / s

Passo 2

Dado o vetor calculado no passo 1, conseguimos calcular o módulo dele da seguinte maneira:

v → = v x f 2 + v y f 2 = 6.5 2 + 5 2 = 67.25 = 8.2 m / s

Passo 3

Agora é possível fazer uma representação dos vetores:

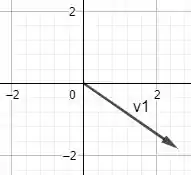
Sendo que v1 é a representação do vetor velocidade em t 1 .

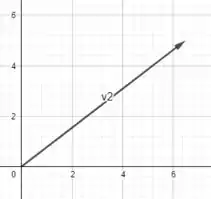
Sendo que v2 é a representação do vetor velocidade em t 2 .

Fica nítido perceber que o sentido, a direção e o módulo dos dois vetores são diferentes.

Sendo assim finalizamos, mais uma questão!! Até a próxima !!

Resposta

  1. a → = 0.39 ,   0.23 m / s ²
  2. 8.2m/s
  3. A representação dos vetores está no passo 3.