Enunciado
Física - John R. Taylor - Introdução à Análise de Erros- Ed: 2º - Capítulo 2.Problemas - Ex. 16
Você aprendeu (ou irá aprender) em ótica que uma lente (especificamente, lentes esféricas delgadas) pode ser caracterizada por um parâmetro chamado comprimento focal f e que se um objeto é posto a uma distância p da lente, a lente forma uma imagem a uma distância q, satisfazendo a equação da lente, 1/f = (1/p) + (1/q), onde f sempre tem o mesmo valor para uma dada lente. Para verificar se estas ideias se aplicam a uma determinada lente, uma estudante coloca uma pequena lâmpada a distâncias variadas de lente e mede a posição q das imagens correspondentes. Ela, então, calcula os valores correspondentes de f a partir da equação da lente e obtém os resultados apresentados na Tabela 2.9. Faça um gráfico de f por p, com barras de erro apropriadas e determine se é verdade que esta lente particular tem uma única distância focal f.
Passo 1
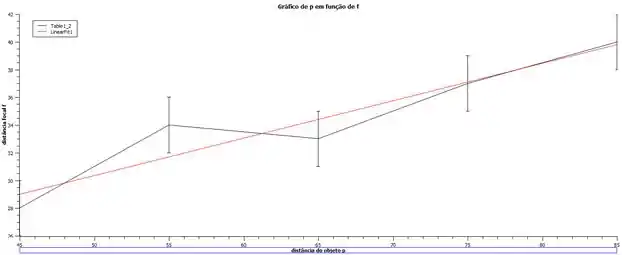
Vamos realizar o gráfico no programa SciDavis, para que você possa entender melhor como ficaria o gráfico com estes dados. Plotamos o gráfico com os resultados obtidos na tabela do problema, obtendo:
Passo 2
Como podemos ver, a reta está, em 3 de 4 pontos, entre as incertezas estabelecidas pelas barras. Por conta disso, podemos entender que está condizente ao esperado e, assim, a lente realmente só apresenta uma distância focal.
Resposta
Ei, a resposta está no passo a passo :)