Quando o volume de um objeto é aumentado, sua área superficial também aumenta. Durante este crescimento, a razão entre metros quadrados e metros cúbicos aumenta ou diminui?
Passo 1
Vamos analisar primeiramente o caso de um cubo que tem suas dimensões lineares aumentadas por um fator x (x>1) da seguinte forma (análogo a dizer que seu volume aumenta):
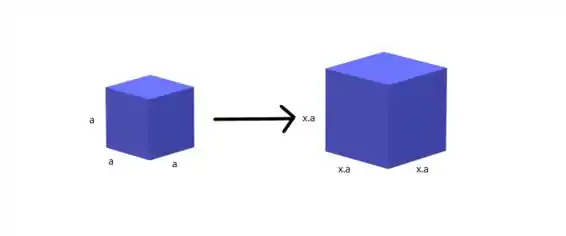
Inicialmente temos:
Após multiplicarmos as dimensões lineares por x:
Razões entre área superficial e volume:
Perceba que, como x é maior que um, seu inverso (1/x) é menor que um. Uma vez que a segunda razão é a primeira multiplicada pelo inverso de x, temos que ela será a menor. Matematicamente:
Portanto, concluímos que quanto um cubo aumenta de volume a razão entre metros quadrados e metros cúbicos diminui.
Passo 2
Para outros sólidos geométricos a demonstração feita no passo 1 pode ser tornar bem mais trabalhosa. Porém, o raciocínio é análogo, sendo fácil perceber que a conclusão será a mesma.
Resposta
Quando o volume de um objeto é aumentado a razão entre metros quadrados e metros cúbicos diminui.