Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 1

10.1 Determine o momento de inércia da área em relação ao eixo x .

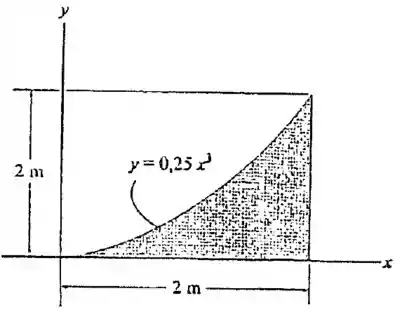
Passo 1

Faaala! Aqui a gente vai aplicar fórmula para achar esse momento de inércia. Vou te mostrar como usa.

A fórmula do momento de inércia em relação ao eixo x é

I x = ∫ A y 2 d A

Nós precisamos um retângulo bem fininho, paralelo ao eixo x , com expessura d y , que esteja dentro da nossa área, desse jeito:

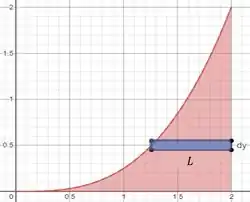
Precisamos achar aquele d A da fórmula, que é a área desse retangulozinho

d A = L d y

A altura a gente já disse que é d y , a largura a gente acha percebendo que

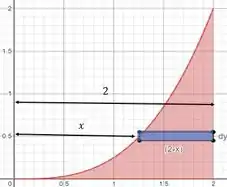
Aí temos:

L = 2 - x

Aí a área do retangulozinho, que a gente chama de elemento infinitesimal de área vai ser igual a

d A = 2 - x d y

Mas precisamos deixar essa área em função de y (já que temos d y ). Isolando x na função dada no enunciado:

y = 0.25 x 3

x 3 = 4 y

x = 4 y 1 / 3

Então

d A = 2 - 4 y 1 / 3 d y

E os limites de integraçãoo vão ir de 0 até 2, porque nossa região está dentro desse intervalo em y .

Passo 2

Agora é só reolver a integral

I x = ∫ A y 2 d A

I x = ∫ 0 2 y 2 2 - 4 y 1 / 3 d y

Vamos abrir a potência, para conseguirmos juntar os y ’s:

I x = ∫ 0 2 y 2 2 - 4 1 / 3 y 1 / 3 d y

I x = ∫ 0 2 2 y 2 - 4 1 / 3 y 2 ⋅ y 1 / 3 d y

Quando a gente multiplica o mesmo numero com expoentes diferentes, devemos somar os expoentes:

I x = ∫ 0 2 2 y 2 - 4 1 / 3 y 2 + 1 / 3 d y

I x = ∫ 0 2 2 y 2 - 4 1 / 3 y 7 / 3 d y

I x = 2 y 3 3 - 4 1 / 3 3 y 10 / 3 10 0 2

I x = 2 2 3 3 - 4 1 / 3 3 2 10 / 3 10

I x = 16 3 - 2 2 3 2 10 3 3 10 = 16 3 - 3 ⋅ 2 4 10 = 16 3 - 3 ⋅ 16 10 = 16 1 3 - 3 10 = 16 10 - 9 30

I x = 16 ⋅ 1 30 = 8 15

I x = 0,533   m 4

Resposta

I x = 0,533   m 4

Ver Outros Exercícios desse livro