Transformação de Tensões

Vamos transformar tensões? Partiu!

Vamos começar olhando essa imagem aqui:

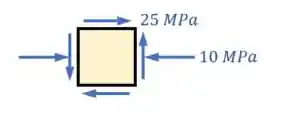
Essa imagem é o que chamamos de estudo plano de tensões, nela temos todas as tensões que atuam no corpo:

• tensões normais : Tensão que atua na direção normal ao plano.
• tensões cisalhantes: : Tensão que atua tangencialmente ao plano.

Até aqui tudo lindo e maravilhoso, MAASSS....

Se você quiser calcular as tensões em um plano que forma um ângulo de com a horizontal, como mostra a imagem abaixo?

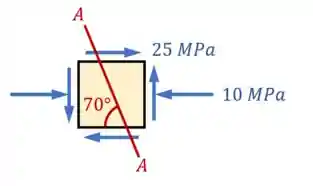
Como resolver?

Através da transformação de tensões!!

O que nós vamos fazer para calcular o que pede no exercício é transformar as tensões que temos.

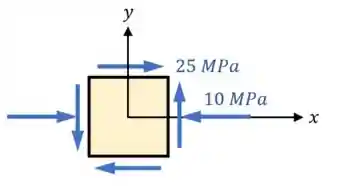
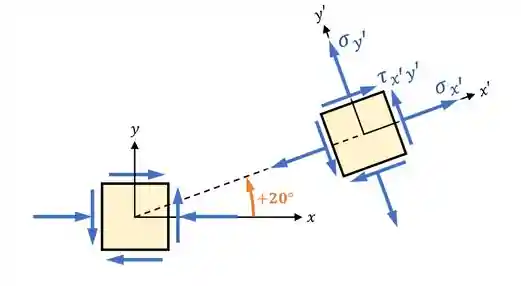
O primeiro passo é definir eixos:

O segundo passo é rotacionar esses eixos, de modo que uma das faces do elemento fique paralela ao plano :

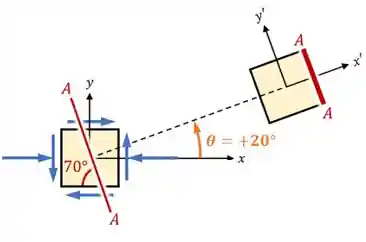
Agora o que vamos fazer é calcular as tensões para o elemento rotacionado:

Fazemos isso usando as seguintes fórmulas:

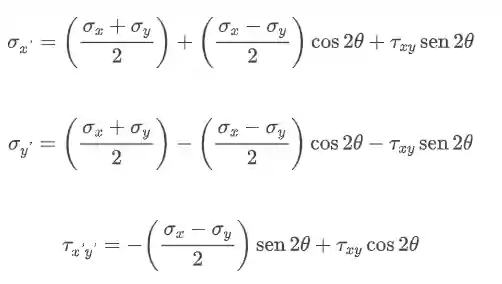
Meio grande as fórmulas não é? Mas não precisa se preocupar não, com o tempo você vai acostumando e também tem algumas dicas de como gravar isso aí!

Quer fixar um pouco mais essa introdução que fizemos? Então confere esse vídeo aqui feito pela equipe maravilhosa do Responde Aí:

Quer continuar vendo conteúdos sobre transformação de tensões e se preparar para a prova?

Então confere, aqui em seguida👇🏽, o nosso Raio-X com o conteúdo todo organizado em capítulos e tópicos e não se arrependa de fechar com a gente 😉