85- Expresse o vetor posição na forma cartesiana; depois determine sua intensidade e os ângulos diretores coordenados.
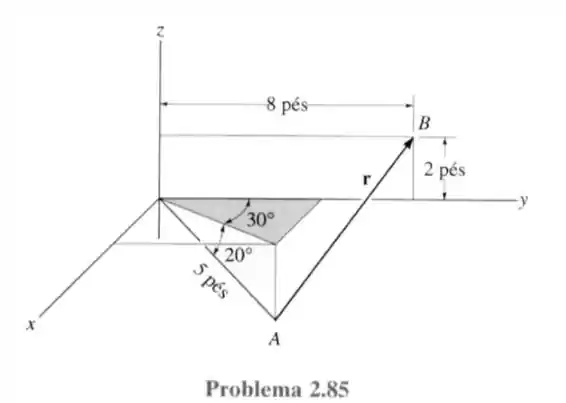
Passo 1
O raciocínio é o mesmo que na questão passada, encontrar os pontos e para depois calcular a posição vetorial, porém o desenho é um pouco diferente. Vamos começar pelo ponto pois é mais simples, esse ponto não tem coordenada estando somente no plano logo:
Já o ponto tem pontos nas três direções e para isso vamos precisar projetar sua distância da origem nos três eixos. Tal como na figura abaixo.
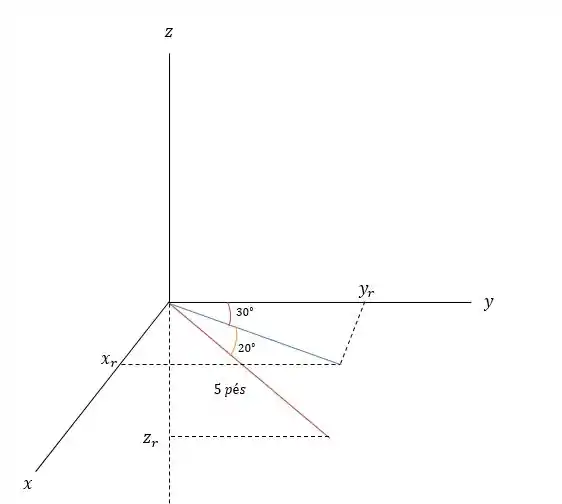
Com isso conseguimos calcular os pontos primeiro vamos para :
Agora vamos projetar a reta vermelha no plano o que dará a reta azul:
E como isso calcular e :
Logo é o ponto:
Passo 2
O vetor tem sentido indo de até , logo vamos diminuir o ponto final do ponto inicial para encontrar a representação cartesiana do vetor :
Agora a intensidade desse vetor será:
Passo 3
E os ângulos de direção desse vetor são: