Uma barra circular AB de comprimento L está fixa contra rotação nas extremidades e carregada por um torque distribuído que varia linearmente em intensidade de zero na extremidade A até na extremidade B (veja a figura).
Obtenha fórmulas para os torques nas extremidades engastadas.
Passo 1
Falaaaaaa meus consagradx’S TUDO NA PAZZZZ???
BORA LAÁAA
Primeiro passa e nosso D.C.L
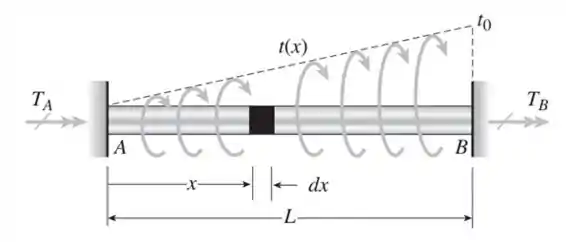
Tomemos o elemento de torque agindo a uma distância da extremidade A.
Passo 2
Encontraremos a expressão para o elemento de torque com o auxilio do D.C.L da barra circular
Integrando o elemento de torque em todo o comprimento para obter a resultante do torque distribuído
Substitua a expressão (1)
Passo 3
Considerando o equilíbrio de torque ao longo do eixo do eixo
Substituindo
Determinaremos o binário reativo elementar no fim da A e B.
Integrando a equação ao longo de todo o comprimento para poder obter o torque reativo na extremidade A.
Da equação (2) , substituiremos
Resolvendo a expressão de integração acima
Portanto, o torque final fixo é de .
Passo 4
Determinaremos o binário reativo elementar no fim da A e B.
Integrando a equação ao longo de todo o comprimento para poder obter o torque reativo na extremidade B.
Da equação (2) , substituiremos
Resolvendo a expressão de integração acima
Portanto, o torque final fixo é de .
Resposta
Portanto, o torque final fixo é de .
Portanto, o torque final fixo é de .