Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 13

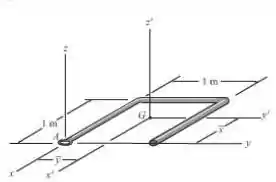
A barra dobrada tem um peso de 100   N / m . Localize o centro de gravidade G ( x - , y - ) e determine os momentos principais de inércia I x ' , I y ' e I z ' da barra em relação aos eixos x ' ,   y ' e z ' .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Por simetria temos que:

y - = 0,5   m

x - é dado por:

x - = ∑ x - W ∑ w

x - = - 1 100 1 + 2 - 0,5 100 1 3 100 ( 1 )

x - = - 0,667   m

Portanto:

I x ' = 2 100 9,81 0,5 2 + 1 12 100 9,81 1 2

I x ' = 5,9463   k g ⋅ m 2

I y ' = 2 1 12 100 9,81 1 2 + 100 9,81 0,667 - 0,5 2 + 100 9,81 1 - 0 , 667 2

I y ' = 3,4   k g ⋅ m 2

I z ' = 2 1 12 100 9,81 1 2 + 100 9,81 0,167 2 + 0,5 2 + 1 12 100 9,81 1 2 + 100 9,81 0,333 2

I z ' = 9,344   k g ⋅ m 2

Resposta

I x ' = 5,9463   k g ⋅ m 2

I y ' = 3,4   k g ⋅ m 2

I z ' = 9,344   k g ⋅ m 2

Ver Outros Exercícios desse livro