Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 3.Problemas - Ex. 48

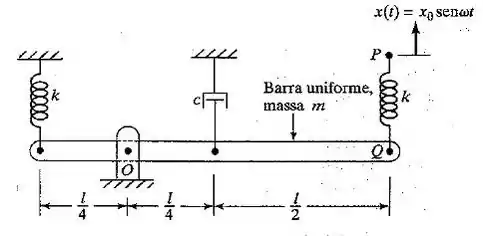
Uma barra uniforme de massa m é articulada no ponto O e apoiada nas extremidades por duas molas, como mostra a Figura 3.53. A extremidade P da mola P Q está sujeita a um deslocamento senoidal, x ( t ) = x 0 sen ω t . Determine o deslocamento angular em regime permanente da barra quando l = 1   m , k = 1.000   N m , c = 500   N ⋅ s m , m = 10   k g , x 0 = 1   c m   e ω = 10 r a d / s

Passo 1

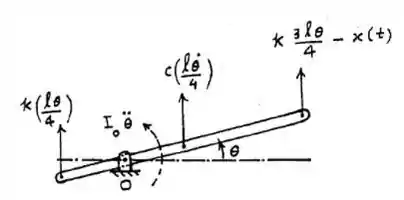
Equação do movimento I 0 θ ¨ = - k l θ 4 l 4 - c l 4 θ ˙ l 4 - k 3 l 4 θ - x ( t ) 3 l 4

i.e.,  I 0 θ ¨ + 1 16 c l 2 θ ˙ + 5 8 k l 2 = 3 4 k l x ( t ) = 3 4 k l x 0 s i n ⁡ ω t (1)

em que I 0 = 1 12 m l 2 + m l 4 2 = 7 48 m l 2 = 7 48 ( 10 ) 1 2 = 1.4583 k g - m 2 (2)

Passo 2

Usando dados fornecidos, Eq. (1) pode ser expresso como

1.4583 θ ¨ + 1 16 ( 500 ) 1 2 θ ˙ + 5 8 ( 1000 ) 1 2 θ = 3 4 ( 1000 ) ( 1 ) ( 0.01 ) s i n ⁡ 10 t

 i.e.,  1.4583 θ ¨ + 31.25 θ ˙ + 625.0 θ = 7.5 s i n ⁡ 10 t (3)

O deslocamento angular de estado estacionário da barra é dado pela Eq. (3.28) com:

θ = 7.5 625.0 - 1.4583 10 2 2 + 31.25 2 10 2 1 2 = 0.01311 r a d

ϕ = t a n - 1 ⁡ 31.25 ( 10 ) 625.0 - 1.4583 10 2 = 0.5779 r a d

Resposta

0.5779 r a d

Ver Outros Exercícios desse livro