Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 1.Problemas - Ex. 48

A base de um motor alternativo está sujeita a movimentos harmônicos nas direções x e y :

x t = X cos ⁡ ω t

y t = Y cos ⁡ ( ω t + ∅ )

Onde X e Y são as amplitudes, ω é a velocidade angular e ∅ é a diferença de fase.

  1. Verifique se a resultante dos dois movimentos satisfaz a equação da elipse dada por:

    2. x 2 X 2 + y 2 Y 2 - 2 x y X Y cos ⁡ ∅     = s e n 2 ∅

  2. Discuta a natureza do movimento resultante dado pela equação (E.1) para os casos especiais de ∅ = 0 ,   ∅ = π 2 ,   e   ∅ = π .

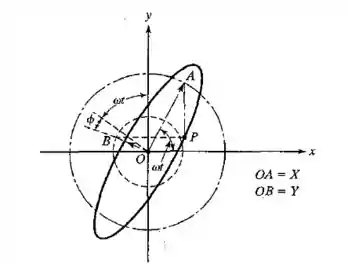
Observação: A figura elíptica representada pela Equação (E.1) é conhecida como uma figura de Lissajous e é útil para interpretar certos tipos de resultados experimentais (movimentos) exibidos por osciloscópios.

Passo 1

Fala, galera. Essa questão é comprida, então vamo pra cima!

Inicialmente nós temos que:

x t = X cos ⁡ ω t

y t = Y cos ⁡ ( ω t + ∅ )

Começando pelo começo, vamos desmembrar o ítem (a).

  1. Pegando a equação dada para x t , jogando o X para o lado esquerdo da equação e elevando tudo ao quadrado temos:

x 2 X 2 = cos 2 ⁡ ω t

Fazendo o mesmo para a equação de y t :

y 2 Y 2 = cos 2   ⁡ ( ω t + ∅ )

Temos que:

2 x y X Y c o s ∅ = 2 cos ⁡ ω t cos ⁡ ω t + ∅   c o s ∅

x 2 X 2 + y 2 Y 2 - 2 x y X Y c o s ∅ = cos 2 ⁡ ω t + cos 2 ⁡ ω t + ∅ - 2   c o s ω t cos ⁡ ∅   cos ⁡ ( ω t + ∅ )

A última equação foi denominada na questão como (E.1).

Passo 2

  1. Ao notar que:

    2. cos 2 ⁡ α = 1 2 ( 1 + cos ⁡ 2 α )

    A eq. (1) pode ser reescrita na forma:

    x 2 X 2 + y 2 Y 2 - 2 x y X Y c o s ∅ = 1 2 + 1 2 cos ⁡ ω t + 1 2 + 1 2 cos ⁡ 2 ω t + 2 ∅ - 2   c o s ω t cos ⁡ ∅   cos ⁡ ( ω t + ∅ )

    = 1 + 1 2   2 cos ⁡ 2 ω t + 2 ω t + 2   ∅ 2 cos ⁡ 2 ω t - 2 ω t - 2 θ 2 - 2 cos ⁡ ω t cos ⁡ ∅ cos ⁡ ( ω t + ∅ )

    = 1 + cos ⁡ 2 ω t + ∅ cos ⁡ ∅ - 2 cos ⁡ ω t cos ⁡ ∅ cos ⁡ ( ω t + ∅ )

    = 1 + cos ⁡ 2 ω t + ∅ cos ⁡ ∅ 1 2 cos ⁡ ω t + ∅ - ω t + cos ⁡ ( ω t + ∅ + ω t

    = 1 + cos ⁡ ∅ cos ⁡ 2 ω t + ∅ - cos ⁡ ∅ cos ⁡ ∅ + cos ⁡ ( 2 ω t + ∅

    = 1 - cos 2 ⁡ ∅ = sin 2 ⁡ ∅

    Essa última equação será denominada por nós como (E.2).

    Passo 3

    Terminado o item (a), podemos começar a desmembrar o ítem (b):

  2. Observamos que quando ∅ = 0 , a eq. (2) se reduz a:

x 2 X 2 + y 2 Y 2 - 2 x y X Y = x X - y Y 2 = 0

Tendo em vista essa igualdade, temos que X = ± X Y y . Isso indica que o padrão do movimento resultante é uma linha reta.

Também temos que quando ∅ = π 2 , a eq. (2) se reduz a:

x 2 X 2 + y 2 Y 2 = 1

Isso demonstra uma elipse com maior eixo na direção x , e menor eixo na direção y

E para ∅ = π , a eq. (2) se reduz a uma linha reta, assim como no caso de ∅ = 0 .

Resposta

  1. Satisfaz.
  2. Para ∅ = 0 e para ∅ = π , temos que o padrão do movimento resultante é uma linha reta; já para ∅ = π 2 , obtém-se uma elipse com maior eixo na direção x , e menor eixo na direção y .
Ver Outros Exercícios desse livro