Um cano de fibra de vidro é içado por um guindaste usando um cabo na forma Y de cabeça para baixo, conforme ilustrado pela figura. O diâmetro externo do cano é 150 mm, sua espessura é 6 mm e seu peso específico é . O comprimento do tubo é e a distância entre os dois pontos de sustentação é .
Determine a tensão fletora máxima no cano devido ao seu próprio peso.
Passo 1
E aiii seres de luz? Bora?
Só vamoo!!
Iniciaremos o exercício determinando o diâmetro interno do tubo usado a relação
Substituindo os valores que o enunciado nos trás, iremos obter
Passo 2
Iremos determinar a área da seção transversal do tubo usando a relação
Substituindo os devidos valores tanto dados pelo enunciado, quanto o que obtivemos no passo anterior, iremos obter o seguinte valor para a área:
Passo 3
Iremos determinar o momento de inércia em relação ao eixo neutro usando a relação
Fazendo as devidas substituições
Passo 4
Determinaremos a intensidade da carga devido ao peso próprio usando a seguinte expressão:
Substituindo valores dados pelo enunciado e os que encontramos no passo anterior:
Passo 5
Iremos agora desenhar o nosso D.C.L do tudo, considerando como a viga suspensa devido ao peso próprio
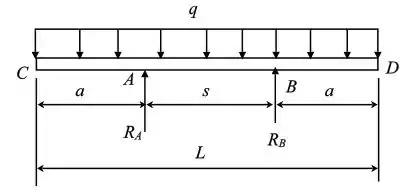
Passo 6
Para determinarmos o comprimento de cada parte suspensa da viga usando a expressão seguinte:
Substituindo os valores dados pelo enunciado,
Passo 7
Agora vamos determinar as reações nos apoios
Considere as forças ao longo da direção vertical.
Devido à simetria,
Desenharemos o diagrama de corpo livre de uma parte AB do feixe tendo uma seção a uma distância de x a partir de C
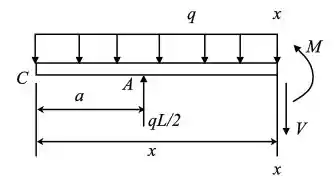
Passo 8
Determinaremos o momento máximo fletor na viga.
Considere o momento sobre a seção .
Substituo
Substituindo os valores
Passo 9
Iremos substituir agora
]
Substituindo os valores:
Passo 10
Determinaremos a tensão máxima de flexão no tubo devido ao próprio peso usando a relação
Substituindo os devidos valores
Resposta
Vide o passo a passo.