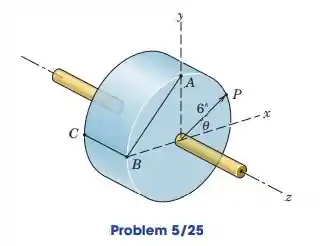
O cilindro sólido gira em torno de seu eixo z. No instante representado, o ponto P na borda tem uma velocidade cuja componente x é , e . Determine a velocidade angular da linha AB na face do cilindro. O elemento linha BC tem uma velocidade angular?
Passo 1
E ai meus queridos? Tudo certinho?
Então vem comigo que no caminho eu explicooo
Já vamos iniciar com o nosso D.C.L do disco circular
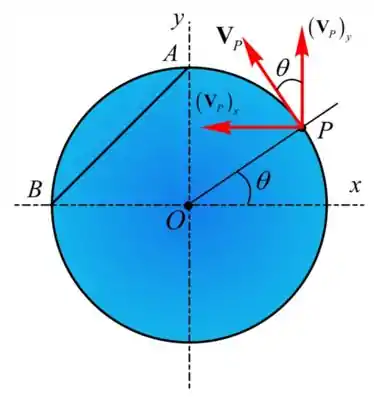
A componente x da velocidade do ponto P é direcionada ao longo do eixo x negativo, o cilindro deve estar girando no sentido anti-horário.
Calculando a velocidade no ponto P, temos
Passo 2
Vamos equacionar a componente x da equação da velocidade
Portanto a velocidade angular do cilindro é de .
Passo 3
Calculando a velocidade angular da linha AB
Portanto, a velocidade angular da linha AB é
A linha BC é paralela ao eixo do cilindro
A velocidade angular do eixo do cilindro é zero
Portanto, a velocidade angular da linha BC é 0.
Resposta
Portanto a velocidade angular do cilindro é de .
Portanto, a velocidade angular da linha AB é
Portanto, a velocidade angular da linha BC é 0.