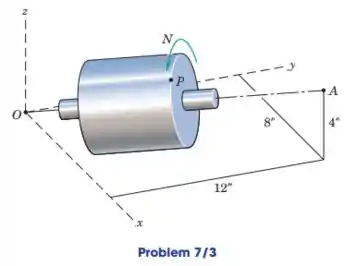
O cilindro sólido está girando em torno do eixo fixo AO com uma velocidade constante na direção mostrada. Se as componentes x e y da velocidade do ponto P são , determine sua componente z da velocidade e a distância radial R de P ao eixo de rotação. Encontre também a magnitude do aceleração de P.
Passo 1
E ai meus queridos? Tudo certinho?
Então vem comigo que no caminho eu explicooo
Sabemos que a velocidade do ponto P, pode e é representada da seguinte maneira
O vetor unitário ao longo da direção da velocidade angular é dado da seguinte maneira
A velocidade angular e a velocidade linear são perpendiculares entre si.
Aplicando o produto escalar para a velocidade angular e a velocidade linear, temos
Portanto, a componente z da velocidade do ponto P é
Passo 2
Calculando o módulo da velocidade linear do ponto P
Calculando a velocidade angular do ponto P
Passo 3
Calculando a distância do ponto P ao centro
Portanto, a distância do ponto P ao centro é de .
Passo 4
Calculando o módulo da aceleração do ponto P
Portanto, o módulo da aceleração do ponto P é de .
Resposta
Portanto, a componente z da velocidade do ponto P é .
Portanto, a distância do ponto P ao centro é de .
Portanto, o módulo da aceleração do ponto P é de .