Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 3.Problemas - Ex. 4

Considere um oscilador harmônico simples. Calcule as médias temporais das energias cinética e potencial em um ciclo e demonstre que essas quantidades são iguais. Por que este é um resultado razoável? A seguir, calcule as médias espaciais das energias cinética e potencial. Discuta os resultados.

Passo 1

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de oscilações.

Item a

A partir do que o enunciado nos pediu, temos que para o:

Tempo médio

A posição e a velocidade de um oscilador harmônico simples são dadas por: x = A s e n   ω 0 t   e   x ˙ = ω 0 A c o s   ω 0 t , sendo ω 0 = k / m

A média temporal da energia cinética é:

T = 1 τ ∫ t t + τ 1 2 m x ˙ 2 d t ,   c o m   τ = 2 π ω 0   s e n d o   o   p e r í o d o   d e   o s c i l a ç ã o

Substituindo a velocidade na equação da energia cinética teremos que:

T = m 2 τ ∫ t t + τ ω 0 A c o s   ω 0 t 2 d t = m 2 τ ω 0 2 A 2 ∫ t t + τ cos 2 ⁡ ω 0 t d t = > T = m 2 τ ω 0 2 A 2 ∙ τ 2 = m ω 0 2 A 2 4

Da mesma forma temos que a média temporal para a energia potencial é:

U = 1 τ ∫ t t + τ 1 2 k x 2 d t = 1 2 τ k ∫ t t + τ A s e n   ω 0 t 2 d t = k 2 τ A 2 ∫ t t + τ s e n 2 ω 0 t d t = k 2 τ A 2 ∙ τ 2 = k A 2 4

Como ω 0 2 = k / m temos que:

U = m ω 0 2 ∙ A 2 4 = K

O resultado indicado é razoável esperando-se a conservação da energia total: E = T + U.

Essa igualdade é válida instantaneamente, assim como na média. Por outro lado, quando T e U são expressos pelas equações iniciais com integral, notamos que eles são descritos exatamente pela mesma função, deslocada por um tempo τ / 2 :

T = m ω 0 2 A 2 2 cos 2 ⁡ ω 0 t   e   U = m ω 0 2 A 2 2 s e n 2 ω 0 t

Portanto, as médias de tempo de T e U devem ser iguais. Então, tomando a média de tempo para E = T + U, encontramos que:

T = U = E 2

Passo 2

Item b

As médias espaciais das energias cinética e potencial são:

T - = 1 A ∫ 0 A 1 2 m x ˙ 2 d x   e   U - = 1 A ∫ 0 A 1 2 k x 2 d x = m ω 0 2 2 A ∫ 0 A x 2 d x

Integrando esta última temos:

U - = m ω 0 2 A 2 6

Para integrar a média espacial da energia cinética fazemos:

x ˙ 2 = ω 0 2 A 2 cos 2 ⁡ ω 0 t = ω 0 2 A 2 1 - s e n 2 ω 0 t = ω 0 2 A 2 - x 2

= > T - = m ω 0 2 2 A ∫ 0 A A 2 - x 2 d x = m ω 0 2 2 A A 3 - A 3 3 = m ω 0 2 A 2 3

Comparando os resultados, temos que:

T - = 2 U -

Para ver que esse resultado é razoável, traçamos T = T(x) e U = U(x):

T = 1 2 m ω 0 2 A 2 1 - x 2 A 2   e   U = 1 2 m ω 0 2 x 2

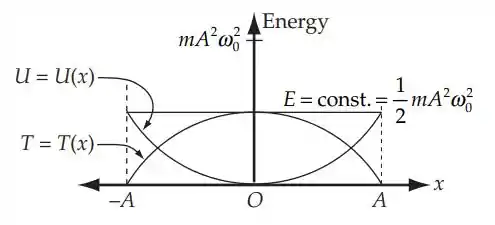
E a área entre T(x) e o eixo x é apenas o dobro da área entre U(x) e o eixo x.

Resposta

Ver passo a passo.