Enunciado
Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 3.Problemas - Ex. 34
Considere um oscilador linear não amortecido com frequência natural se a função degrau . Calcule e desenhe a função resposta para uma função de força de impulso atuando durante um tempo . Forneça uma interpretação física dos resultados.
Passo 1
Faala meu povo, bora com tudo pra mais uma questão do nosso livro!
Primeiramente precisamos desenhar a função de resposta para uma função de força de impulso para um oscilador linear não amortecido, com , , e , a função de resposta é:
para
Quando , nós temos:
Para substituímos por e na equação 3.108 do nosso livro, então temos:
Mas temos , assim:
Dessa forma:
usando as equações (1), (2) e (3), e também os valores dados, podemos desenhar a função resposta como uma função de . Para plotar a função usaremos python e o código é mostrado na imagem a seguir:
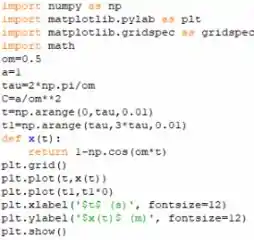
Na terminação do impulso, o oscilador é retornado à sua condição de equilíbrio, porque o impulso retém exatamente um período do oscilador e o oscilador não é amortecido
E assim a gente conclui e nossa questão, te vejo na próxima!