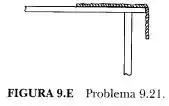
Uma corda flexível com comprimento de 1,0 m desliza sobre um tampo de mesa sem atrito, como mostra a Figura 9.E. Ela é inicialmente liberada do repouso com 30 cm pendendo da borda da mesa. Determine o tempo no qual a ponta esquerda da corda alcança a borda da mesa.

Começamos com a equação do movimento. Vamos chamar de a parte que está pendendo e de o comprimento total da corda. Assim, a força vai ser

Igualando isso a massa vezes a aceleração, temos

Onde é a forma da aceleração, que é a derivada segunda da posição. Simplificando a massa, temos

Agora temos uma equação diferencial. Resolvendo-a, temos que uma das soluções possíveis é

Isolando nessa equação e considerando que quando toda a corda está fora da mesa, temos vamos achar

Por fim, pela solução da equação diferencial, sabemos que . Substituindo os valores, encontramos