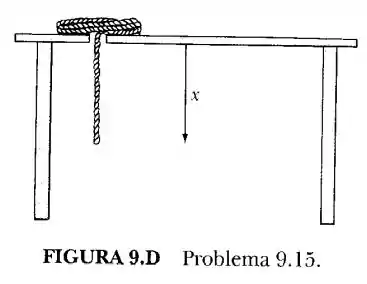
Uma corda lisa é colocada sobre um furo em uma mesa (Figura 9.D). Uma ponta da corda cai através do furo em t= 0, puxando continuamente o restante da corda. Determine a velocidade e a aceleração da corda como função da distância até a ponta da corda x. Ignore qualquer atrito. O comprimento total da corda é L.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de dinâmica de um sistema de partículas.
A partir do que o problema pede, temos:
onde m é a massa de comprimento x da corda. Então:
Tentamos uma solução de lei de potência:
Daí, teremos que:
Como isso deve ser verdade para todo x, o expoente e o coeficiente de x devem ser os mesmos em ambos os lados da equação.
Assim temos que 2n = 1 ou n = 1/2. E obtemos:
Reescrevendo e integrando teremos que:
Resposta
Ver passo a passo.