Enunciado

Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 4.9 - Ex. 2(2)vi

Deduza a Equação 7.52 convertendo, em primeiro lugar, o circuito equivalente de Norton, para um equivalente de Thévenin e, então, somando as tensões ao longo do laço fechado, usando a corrente i do capacitor como a variável relevante.

Use a técnica de separação de variáveis para determinar a solução para a Equação 7.52. Verifique se sua solução está de acordo com a da Equação 7.53.

Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre resposta de circuitos RL e RC de primeira ordem!

Nesse item, podemos começar ilustrando nossa situação:

Com isso, podemos escrever que:

E também:

Ou seja:

Passo 2

Começamos com as seguintes relações:

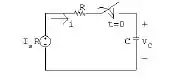
Com isso, podemos escrever que:

Com isso, fica fácil chegar na solução de:

Resposta