Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 6.Problemas - Ex. 23

Deduza as equações de movimento para a corda firmemente esticada que sustenta três massas, como mostra a Figura 6.28. Considere que as extremidades da corda sejam fixas.

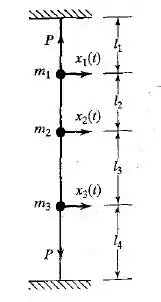
Passo 1

Falaaa meus amigos! Como vocês estão? Vamos pra mais uma questãozinha desse assunto?

Inicialmente deixando claro que assumiremos pequenas deflexões, portanto, a tensão em P na figura permanece constante.

Suporemos três diferentes situações para o valor de forças, cada ilustração a seguir representará uma delas:

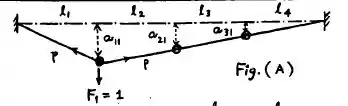
Como mostrado na figura, nós temos que F 1 = 1 ,   F 2 = F 3 = 0 .

Fazendo o equilíbrio de forças verticais, temos que:

F 1 = 1 = a 11 l 1 P + a 11 l 2 + l 3 + l 4 P

a 11 = 1 P 1 l 1 + 1 l 2 + l 3 + l 4

Por definição da regra de semelhança de triângulos, nós temos que:

a 11 l 2 + l 3 + l 4 = a 21 l 3 + l 4 = a 31 l 4

Passo 2

Agora vamos para segunda suposição:

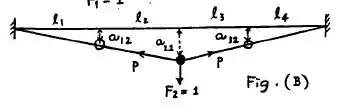
Segundo essa suposição ilustrada, temos que F 2 = 1 ,   F 1 = F 3 = 0 . Fazendo o equilíbrio vertical de forças, nós temos que:

F 2 = 1 = a 22 l 1 + l 2 P + a 22 l 3 + l 4 P → a 22 = 1 P 1 l 1 + l 2 + 1 l 3 + l 4

Da semelhança de triângulos, temos que:

a 12 = l 1 l 1 + l 2 a 22   ,   a 32 = l 4 l 3 + l 4 a 22

Passo 3

Para a terceira suposição:

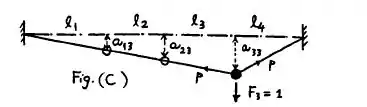
Nesse caso, F 3 = 1 ,   F 1 = F 2 = 0 . Para o equilíbrio de forças verticais, temos:

F 3 = 1 = a 33 l 1 + l 2 + l 3 P + a 33 l 4 P ; a 33 = 1 P 1 l 1 + l 2 + l 3 + 1 l 4

De semelhança de triângulos, temos que:

a 23 = l 1 + l 2 l 1 + l 2 + l 3 a 33 ; a 13 l 1 l 1 + l 2 + l 3 a 33

Assim, temos que a m ω → ¨ + ω → = 0 → .

Com:

m = m 1         0           0 0             m 2         0 0             0               m 3 ; ω → = ω 1 ω 2 ω 3   .

Resposta

Assim, temos que a m ω → ¨ + ω → = 0 → .

Com:

m = m 1         0           0 0             m 2         0 0             0               m 3 ; ω → = ω 1 ω 2 ω 3   .

Ver Outros Exercícios desse livro