Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 6.Problemas - Ex. 22

Deduza as matrizes de flexibilidade e rigidez do sistema massa-mola mostrado na Figura 6.27 considerando que todas as superfícies de contato sejam desprovidas de atrito.

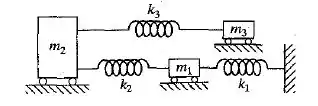
Passo 1

Falaaa meus amigos! Como vocês estão? Vamos pra mais uma questãozinha desse assunto?

Inicialmente trataremos da matriz de flexibilidade.

Chamaremos por a 11 a deflexão da massa m 1 , isso sabendo que temos m 1 = 1 k 1 ( m 2   e   m 3 possuem o mesmo deslocamento já que não tem outras forças ou restrições, ok?)

Dessa forma, nós temos que:

a 21 = a 31 = 1 k 1

Usando o princípio da rigidez equivalente, aplicando carga unitária a m 2 , nós temos que:

1 k e q = 1 k 1 + 1 k 2

a 22 = 1 k e q = 1 k 1 + 1 k 2

Já que a m 3 segue a deflexão de m 3 , nós temos que a 32 = a 22 .

Agora, novamente aplicando a carga unitária, mas dessa vez a m 3 , temos que:

1 k e q = 1 k 3 + 1 k 1 + 1 k 2

a 33 = 1 k e q = 1 k 1 + 1 k 2 + 1 k 3

Agora, já podemos montar a matriz de flexibilidade, ajustando cada componente no seu devido lugar.

Passo 2

Agora vamos tratar da matriz de rigidez, galera. Vamos denominar três possíveis deslocamentos pra cada uma das massas, se chamarão x 1 , x 2   e   x 3 , como na ilustração:

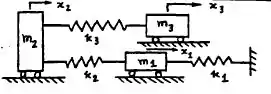
Agora vamos supor três situações com esses deslocamentos, para cada um obteremos os componentes da nossa matriz, por meio das três forças:

  1. x 1 = 1 ,   x 2 = x 3 = 0 :

    2. F 1 = k 1 + k 2 = k 11

    F 2 = - k 2 = k 21

    F 3 = 0 = k 31

  2. x 2 = 1 ,   x 1 = x 3 = 0 :

    3. F 1 = - k 2 = k 12

    F 2 = k 2 + k 3 = k 22

    F 3 = - k 3 = k 23

  3. x 3 = 1 ,   x 2 = x 3 = 0 :

F 1 = 0 = k 13

F 2 = - k 3 = k 23

F 3 = k 3 = k 33

Resposta

a =             1 k 1                                           1 k 1                                               1 k 1 1 k 1                                 1 k 1 + 1 k 2         1 k 1 + 1 k 2 1 k 1                     1 k 1 + 1 k 2     1 k 1 + 1 k 2 + 1 k 3

k = k 1 + k 2             - k 2                         0 - k 2                 k 2 + k 3     - k 3 0                             - k 3                                         k 3

Ver Outros Exercícios desse livro