Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 1.Problemas - Ex. 2

Demonstre as equações 1.10 e 1.11 a partir de considerações trigonométricas

Passo 1

Fala, galera, mais uma em... Essa é pra demonstrar duas equações que estão lá no livro.

A primeira (1.10) é essa aqui:

cos 2 ⁡ α + cos 2 ⁡ β + cos 2 ⁡ γ = 1

Onde α ,   β ,   γ são como segue:

Bora pra CIMAA.

a 1 = a . cos ⁡ α

b 1 = a . cos ⁡ β

c 1 = a . cos ⁡ γ

Vamos elevar as equações mostradas ao quadrado e somar termo a termo:

a 1 2 + b 1 2 + c 1 2 = a 2 cos 2 ⁡ α + cos 2 ⁡ β + cos 2 ⁡ γ

Mas também podemos ver que:

a 1 2 + b 1 2 = k 2

k 2 + c 1 2 = a 2

De onde tiramos que a 1 2 + b 1 2 + c 1 2 = a 2

Assim:

cos 2 ⁡ α + cos 2 ⁡ β + cos 2 ⁡ γ = 1

c.q.d.

Uurrrraaaa!!

Passo 2

Agora vamos demonstrar a 1.11.

cos ⁡ θ = cos ⁡ α ⋅ cos ⁡ α ' + cos ⁡ β ⋅ cos ⁡ β ' + cos ⁡ γ ⋅ cos ⁡ γ '

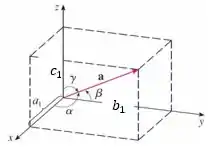
Onde θ é um ângulo formado por duas linhas L 1 e L 2 que têm cosseno diretores α ,   β ,   γ e α ' ,   β ' ,   γ ' respectivamente.

Vamos dar nossos pulos nessa questão, usar a estratégia da esperteza.

O ângulo entre L 1 e L 2 é o mesmo ângulo formado pelos vetores unitários na direção de L 1 e L 2 , estou certo? SIIIMM!

Sendo assim, esses vetores unitários, que nós vamos chamar de u 1 → e u 2 → , têm componentes:

u 1 → = ( cos ⁡ α , cos ⁡ β , cos ⁡ γ )

u 2 → = ( cos ⁡ α ' , cos ⁡ β ' , cos ⁡ γ ' )

Agora façamos o produto escalar entre esses dois vetores:

u 1 → ⋅ u 2 → = u 1 → . u 2 → . cos ⁡ θ

Hahaa, tá de brinks, apareceu o ângulo que a gente quer bem ali.

Só que lembra que u 1 → e u 2 → são vetores unitários, daí: u 1 → = u 2 → = 1

Temos então:

u 1 → ⋅ u 2 → = cos ⁡ θ → cos ⁡ α , cos ⁡ β , cos ⁡ γ ⋅ cos ⁡ α ' , cos ⁡ β ' , cos ⁡ γ ' = cos ⁡ θ

Finalmente:

cos ⁡ θ = cos ⁡ α ⋅ cos ⁡ α ' + cos ⁡ β ⋅ cos ⁡ β ' + cos ⁡ γ ⋅ cos ⁡ γ '

c.q.d.

VAAPOOOO!!!

Por essa você não esperava em, diz aí... rsrsrsrs

Resposta

Demomstrações